При малых расстройках
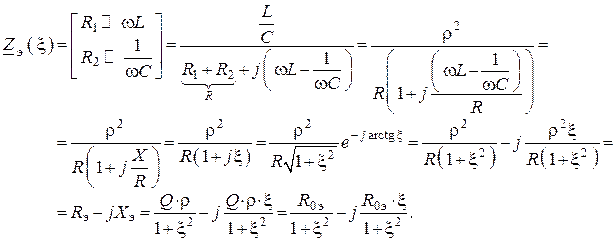
4. Полное эквивалентное сопротивление на любой и резонансной частоте
.
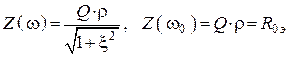5. Фазо-частотная характеристика (ФЧХ) (рис. 80)
.
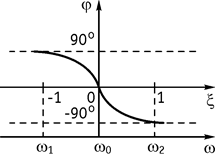
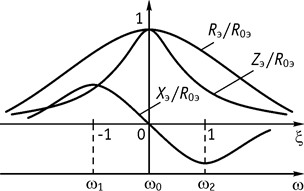
Рис. 80 Рис. 81
6. Графики частотных характеристик: Rэ, Хэ, Zэ нормированных относительно R0э (рис. 81).
7. Комплексные действующие значения токов в ветвях на любой частоте и резонансной частоте
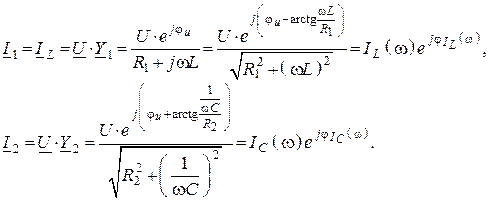
На резонансной частоте
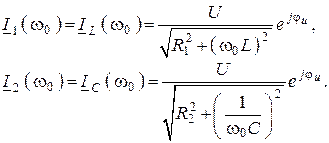
8. Действующие значения токов в ветвях на резонансной частоте
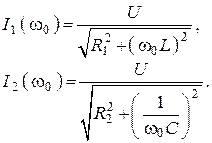
9. Комплексные действующие значения входного тока для малых расстроек и на резонансной частоте
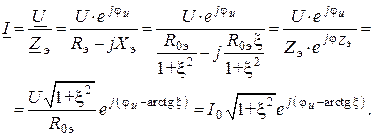
На резонансной частоте
.
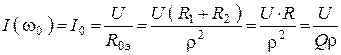10. Отношение действующего значения тока ветвей к действующему входному току
.
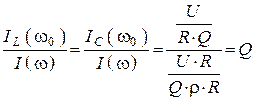– резонанс токов (токи в ветвях в Q раз больше входного тока).
11. КПФ по току – отношение токов в ветвях и входного тока
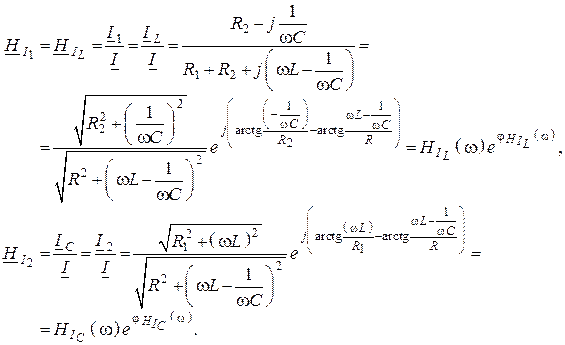
Учитывая малые расстройки, малые потери запишем передаточные функции по току (АЧХ и ФЧХ)
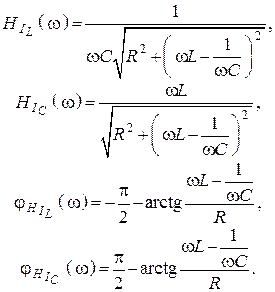
12. Влияние сопротивления генератора на свойства параллельного контура
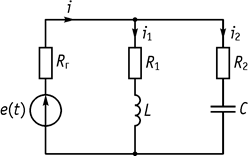
Рис. 82
Порядок анализа схемы, приведенной на рисунке 82
1. Определяем напряжение контура на любой частоте
.
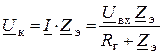2. Определяем напряжение контура на резонансной частоте
.
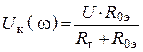3. Найдем отношение напряжения контура 
к напряжению контура на частоте
резонанса 
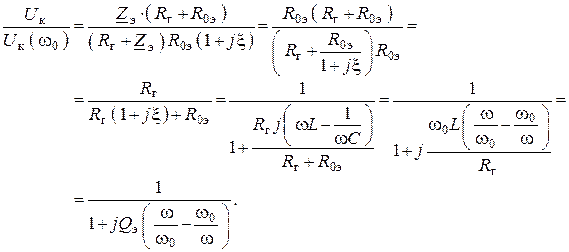
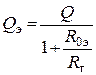
– эквивалентная добротность параллельного контура.
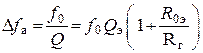
– абсолютная полоса пропускания.
.
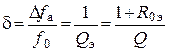Из формул видно, что
добротность параллельного контура, имеющего Rг, меньше добротности последовательного контура.
1. В принципе эта добротность приближается к добротности последовательного контура, если Rг ® ¥.
2. Полоса пропускания шире полосы пропускания последовательного контура.
3. Последовательный контур необходимо запитывать источником напряжения, а параллельный источником тока.
Параллельный контур без потерь
Параллельный
контур без потерь приведен на рисунке 83.
1. R1 = 0.
2. R2 = 0.
3. Резонансная частота
.
4. Комплексные токи в ветвях
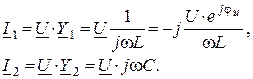
5. Комплексная проводимость контура
.
6. Реактивная проводимость ветвей
.
7. Реактивная проводимость контура
.
8. Входной ток
.
9. Эквивалентное сопротивление на резонансной частоте
.
10. Реактивное сопротивление на резонансной частоте
.
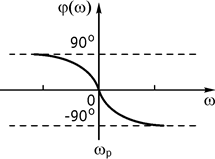
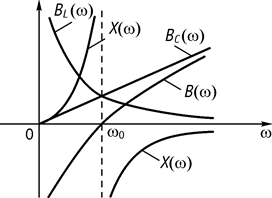
Рис. 84 Рис. 85
11. ФЧХ (рис. 84)
.
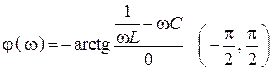12. Графики зависимостей 
приведены
на рисунке 85.
Индуктивно связанные колебательные контуры
Имеют более широкую полосу по сравнению с одиночными контурами и лучшую избирательность.
Схемы замещения
1. Т-образная (рис. 86, а)
2. П-образная (рис. 86, б)
Замечание: переход от Т к П и наоборот производится по формулам аналогичным формулам перехода от «звезды» к «треугольнику» и наоборот.
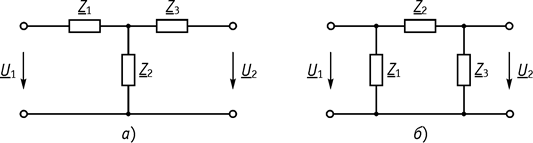
Рис. 86
Классификация связанных контуров по виду связи
1. Контуры с трансформаторной связью (рис. 87).
Коэффициент связи контуров определяется как среднее геометрическое коэффициентов передачи по напряжению, слева направо и справа налево в режиме соответственно холостого хода.
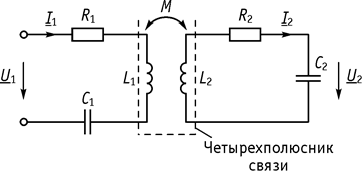
Рис. 87
Для трансформаторной связи
.
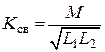2. Контуры с автотрансформаторной связью (рис. 88).
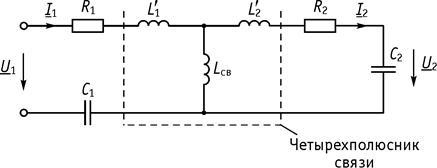
Рис. 88
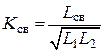, где 
,
.
3. Контуры с внутренней емкостной связью.
4. Контуры с внешней емкостной связью.
5. Контуры с внешней индуктивной связью.
6. Контуры с комбинированной связью.
Замечание: поскольку свойства связанных контуров при определенных условиях идентичны друг другу, то мы рассмотрим подробно свойства контуров с трансформаторной связью.
Контуры с трансформаторной связью
Схема приведена на рисунке 89.
Цель анализа: определить параметры и частотные характеристики.
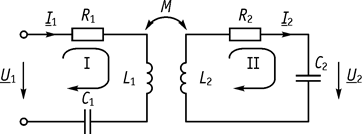
Рис. 89
Замечание: при анализе будем использовать одноконтурные схемы замещения и соответствующие уравнения.
1. Выделяем контуры, обходы, ЗНК
2. Решая уравнения, определяем токи
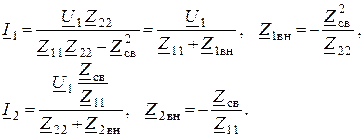
3. Виды резонанса:
а) Первый частный резонанс, наступает при выполнении условия
.
При настройке 1-го контура
.
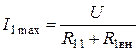б) Второй частный резонанс, достигается настройкой 2-го контура до выполнения условия
,
.
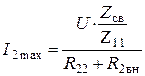в) Сложный резонанс, достигается настройкой 1-го и 2-го контуров до выполнения условия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.