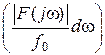
и начальными фазами ![]() .
.
Физический смысл прямого преобразования Фурье (спектра сигнала)
Установим, используя выражение комплексной амплитуды
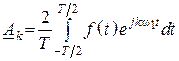 .
.
Возьмем предел слева и справа
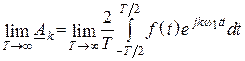 , при этом учтем
, при этом учтем
![]() ,
, ![]() ,
, ![]() .
.
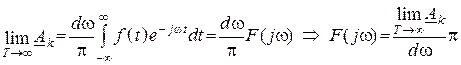 .
.
Видно, что ![]() – это отношение
предела комплексной амплитуды к малому диапазону частот
– это отношение
предела комплексной амплитуды к малому диапазону частот ![]() –
спектральная плотность комплексной амплитуды.
–
спектральная плотность комплексной амплитуды.
Основные свойства преобразования Фурье
1. Если ![]() – четная, то спектр
– четная, то спектр ![]() – вещественный и
– вещественный и
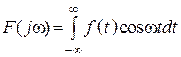 .
.
2. Если ![]() – нечетная, то
– нечетная, то ![]() –
мнимый
–
мнимый
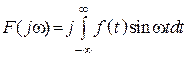 .
.
3. Если ![]() – четная, то в спектре можно поменять
«–» на «+»
– четная, то в спектре можно поменять
«–» на «+»
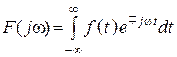 .
.
4. Свойства взаимозаменяемости
![]()
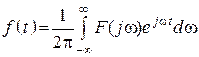 ;
; 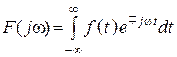 .
.
Это свойство позволяет установить связь между
временными и частотными характеристиками сигнала, в частности, если сигнал ![]() – прямоугольный импульс (рис. 123).
– прямоугольный импульс (рис. 123).
5. ![]() может
быть задана как
может
быть задана как ![]() , либо
, либо ![]() , либо амплитудным спектром
, либо амплитудным спектром ![]() , либо фазовым
, либо фазовым ![]() .
Причем существует однозначная связь между модулем и фазой, между мнимой и
действительной частями спектра. Эту связь можно показать на одностороннем
сигнале, при этом
.
Причем существует однозначная связь между модулем и фазой, между мнимой и
действительной частями спектра. Эту связь можно показать на одностороннем
сигнале, при этом
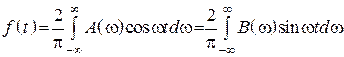 .
.
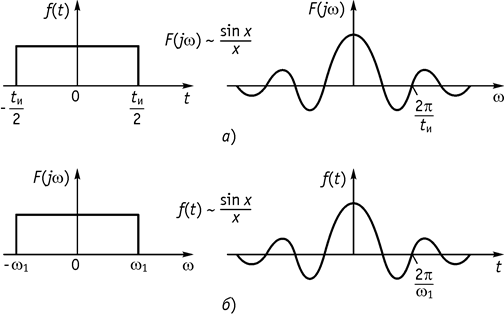
Рис. 123
Поскольку:
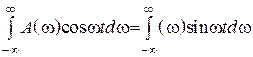 .
.
Замечание 1: на нулевой частоте (w = 0)
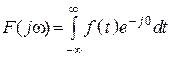 .
.
Замечание 2: временное и спектральное представление сигнала это математические модели одного и того же физического процесса.
Замечание 3: между преобразованием Фурье и Лапласа существует связь, которая позволяет, зная преобразование Фурье записать преобразование Лапласа, и зная преобразование Лапласа записать преобразование Фурье.
Покажем связь для одностороннего сигнала
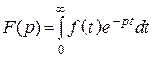 –
Лапласа,
–
Лапласа,
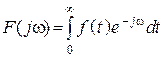 –
Фурье.
–
Фурье.
Имеем
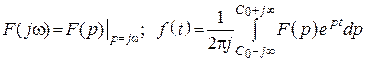 – Лапласа,
– Лапласа,
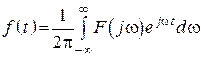 – Фурье, имеем
– Фурье, имеем
![]() .
.
Основные теоремы преобразования Фурье
1. Теорема линейности
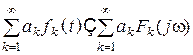 .
.
2. Теорема сдвига
![]() .
.
3. Теорема изменения масштаба
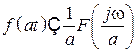 .
.
4. Теорема
свертки: произведение двух функций ![]() и
и ![]() соответствует свертке их спектров
соответствует свертке их спектров
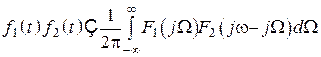 .
.
5. Произведение спектров двух сигналов соответствует свертке сигналов
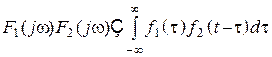 .
.
6. Смещение спектров по частоте
![]() .
.
7. Дифференцирование и интегрирование функций
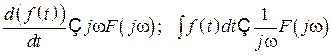 .
.
Замечание: последние две формулы справедливы, если сигнал имеет полубесконечную протяженность.
Методы определения спектра сигналов
1. Формула прямого преобразования Фурье
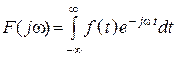 .
.
2. Численные методы.
3. Инструментальные методы.
![]()
Спектры наиболее распространенных сигналов
1. Единичная импульсная функция:
![]()
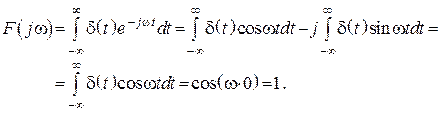
![]() .
.
![]() – амплитудный
спектр (рис. 124, а).
– амплитудный
спектр (рис. 124, а).
![]() – фазовый спектр (рис. 124, б).
– фазовый спектр (рис. 124, б).
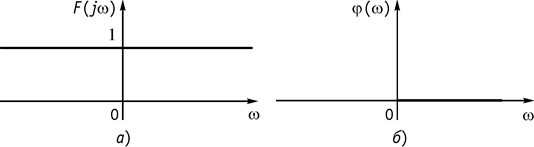
Рис. 124

Рис. 125
Замечание: зная спектр, найдем обратную d-функцию
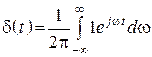 .
.
Используя свойства взаимозаменяемости ![]()
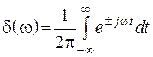 .
.
2. Постоянная функция ![]()
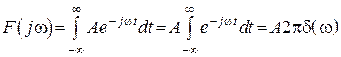 .
.
Амплитудный спектр представлен на рисунке 125, а, фазовый спектр на рисунке 125, б.
3. Единичная функция (рис. 126, а):
![]()
Видно, что данная функция не удовлетворяет условиям
абсолютной интегрируемости, поэтому для определения спектра умножают эту
функцию на экспоненциальную ![]() .
.
![]() – удовлетворяет
условию абсолютной интегрируемости. Определяет спектр этой функции, а потом
берут предел при
– удовлетворяет
условию абсолютной интегрируемости. Определяет спектр этой функции, а потом
берут предел при ![]() и получают спектр единичной
функции.
и получают спектр единичной
функции.
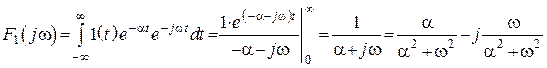 .
.
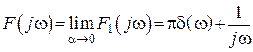 ,
,
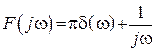 – для
– для ![]() .
.
Амплитудный спектр единичной функции приведен на рисунке 126, б, фазовый спектр на рисунке 126, в).
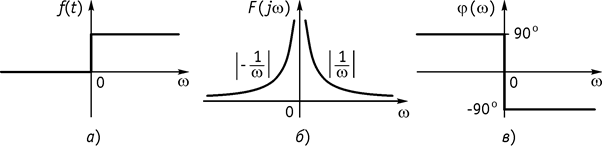
Рис. 126
Найдем обратным преобразованием сигнал, зная спектр
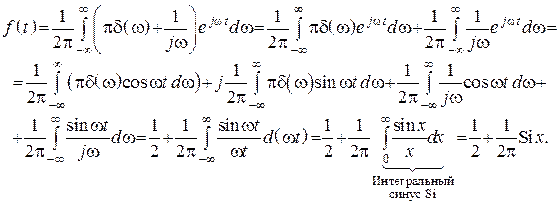
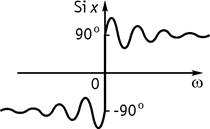
Рис. 127
Интегральный синус изображен на рисунке 127.
4. Гармонические колебания а) ![]() (рис. 128, а).
(рис. 128, а).
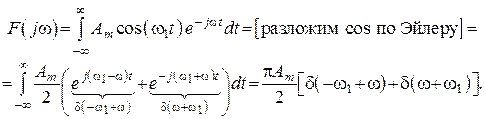
б) ![]() (рис. 128, б).
(рис. 128, б).
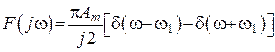 .
.
Модуль амплитудного спектра приведен на рисунке 129.
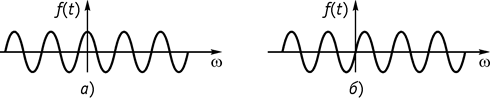
Рис. 128
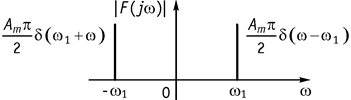
Рис. 129
5. Функция – прямоугольный одиночный импульс (рис. 130, а)
![]()
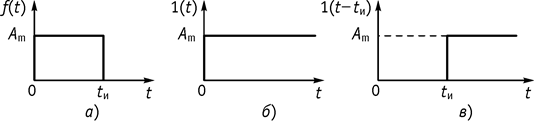
Рис. 130
Найдем спектр, подставляя разность двух единичных
функций, сдвинутых на длительность импульса ![]() (рис.
130, б, в).
(рис.
130, б, в).
Зная спектр единичной функции, и используя время запаздывания
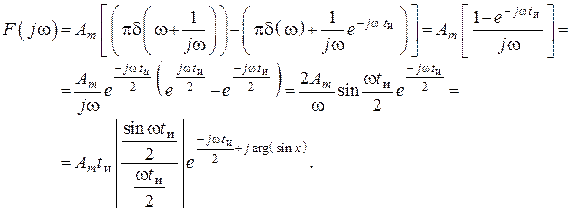
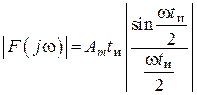 – амплитудный спектр (рис.
131, а).
– амплитудный спектр (рис.
131, а).
![]() – фазовый спектр (рис. 131, б).
– фазовый спектр (рис. 131, б).
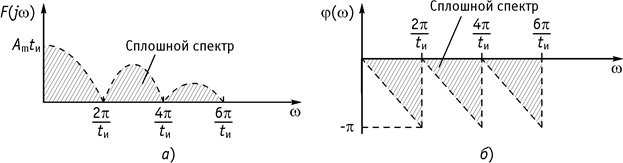
Рис. 131
Методы определения сигнала по спектру
1. Использование формулы обратного преобразования Фурье
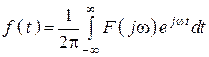 .
.
2. Метод, основанный на вычетах функции
Вычеты берутся от спектральной функции
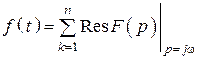 .
.
3. Метод, основанный на разложении спектральной функции на простые дроби
Замечание: ![]() переводится в
переводится в ![]() заменой
заменой ![]()
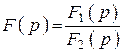 .
.
Определяются корни ![]() .
Эти корни являются полюсами функции
.
Эти корни являются полюсами функции ![]() . В зависимости от
полюсов применяются формулы из лекции 16, затем подстановкой
. В зависимости от
полюсов применяются формулы из лекции 16, затем подстановкой ![]() находим
находим ![]() от
переменной
от
переменной ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.