![]() .
.
3. Найдем выходной сигнал как сумму реакций на входные импульсы
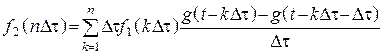 .
.
4. Перейдем к пределу при Dt ® 0
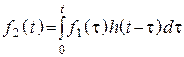 ,
,
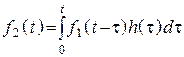 .
.
Анализ переходных процессов в цепях первого порядка методом интеграла свертки
1. Пусть дана схема, приведенная на рисунке 115.
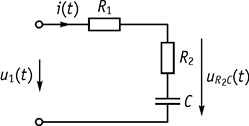
Рис. 115
На вход поступает прямоугольный импульс
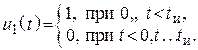
Необходимо найти реакцию цепи (выходное напряжение) ![]() методом интеграла
свертки
методом интеграла
свертки
1. Определяем
импульсную характеристику ![]() . Если была бы
известна
. Если была бы
известна ![]() , то:
, то:
![]() .
.
Если неизвестно, то надо найти ![]() ,
затем
,
затем ![]()
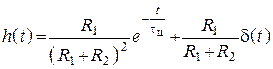 .
.
2. Определяем участки
интегрирования а) ![]() ,
, ![]()
б) ![]() .
.
3. Находим реакцию на первом участке
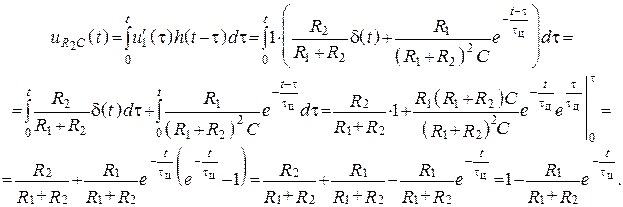
4. Находим реакцию на втором участке, учтем п. 3
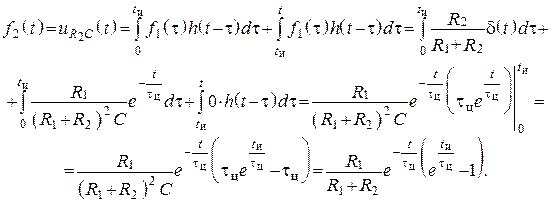
5. График при ![]() ,
, ![]() приведен
на рисунке 116.
приведен
на рисунке 116.
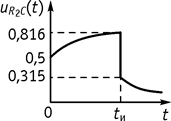
Рис. 116
При определении ![]() и
и ![]() мы полагали, что начальные условия равны
0, если неравны 0, то они учитываются в схеме в виде эквивалентных источников
тока и напряжения.
мы полагали, что начальные условия равны
0, если неравны 0, то они учитываются в схеме в виде эквивалентных источников
тока и напряжения.
Интегрирующие пассивные цепи
Интегрирующие пассивные цепи – это цепи у которых реакция пропорциональна интегралу воздействия. Как правило, это цепи RL и RC.
Анализ RL и RC цепей во временной области приведен в таблице 7.
Таблица 7
|
Цепь RС |
Цепь RL |
|
|
|
|
1. ЗНК |
|
|
|
|
|
2. Условия интегрирования во временной области |
|
|
|
|
|
3. Учитывая условия интегрирования, записываем ЗНК |
|
|
|
|
|
4. Определяем ток в цепи |
|
|
|
|
|
5. Записываем выходное напряжение. Видно, что выходное напряжение эквивалентно интегралу входного напряжения |
|
|
|
|
|
6. Пусть на вход подается последовательность прямоугольных импульсов. Тогда на выходе реакция будет иметь вид |
|
|
|
|
Анализ RL и RC цепей в частотной области приведен в таблице 8.
Таблица 8
|
Цепь RС |
Цепь RL |
|
|
|
|
1. Комплексная передаточная функция |
|
|
|
|
|
2. При
идеальном интегрировании |
|
|
|
|
|
3. С учетом 2 запишем 1 |
|
|
|
|
|
4. Зная H, определим выходное напряжение |
|
|
|
|
Дифференцирующие пассивные цепи
Дифференцирующие пассивные цепи – эквивалентные цепи, реакция которых эквивалентна производной воздействия. Как правило, это цепи RL и RC.
Анализ RL и RC цепей во временной области приведен в таблице 9.
Таблица 9
|
Цепь RС |
Цепь RL |
|
|
|
|
1. ЗНК |
|
|
|
|
|
2. Условия интегрирования во временной области |
|
|
|
|
|
3. Учитывая 2, записываем 1, откуда определяем |
|
|
|
|
|
4. Находим выходное напряжение |
|
|
|
|
![]() Частотный (спектральный) метод
анализа линейных
электрических цепей
Частотный (спектральный) метод
анализа линейных
электрических цепей
Различают:
1. Частотный метод анализа при периодическом негармоническом воздействии, например, воздействие вида последовательности прямоугольных импульсов, вида треугольных импульсов (рис. 117).
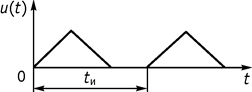
Рис. 117
В этом случае входная последовательность (сигнал) представляется в виде ряда Фурье.
2. Частотный анализ при воздействии непериодического, негармонического воздействия, например, одиночный прямоугольный (рис. 118, а) или треугольный импульс (рис. 118, б).
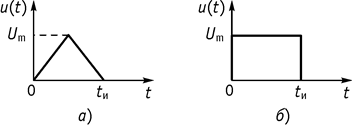
Рис. 118
В этом случае входной сигнал представляется в виде интеграла Фурье.
Ряды Фурье
Если ![]() удовлетворяет
условиям Дирихле:
удовлетворяет
условиям Дирихле:
1. Имеет на периоде конечное число разрывов.
2. Имеет конечное число максимумов и минимумов, то она может быть разложена в ряд Фурье
3 формы ряда Фурье
1. Тригонометрическая форма а) 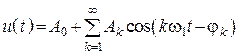 ;
;
б) 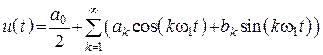 , где
, где ![]() –
среднее значение функции за период (постоянная составляющая);
–
среднее значение функции за период (постоянная составляющая);
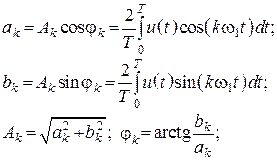
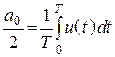 –
постоянная составляющая.
–
постоянная составляющая.
2. Комплексная форма ряда Фурье.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.