Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 11

а)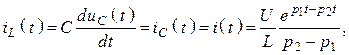

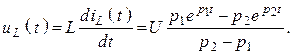
б)

в)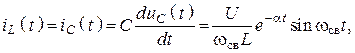

.

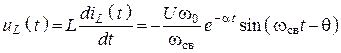16. Нарисуем графики для случаев а, б, в.

а) Для корней вещественных и различных графики напряжений и тока изображены на рисунке 97, а.

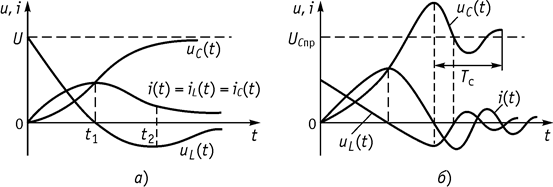
Рис. 97

б) Графики совпадают с пунктом а (рис. 97, а).

в) Графики напряжений и тока представлены на рисунке 97, б.

Замечание 1: время 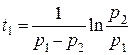  определяется из производной тока приравненной к нулю

.

Время .

 – коэффициент затухания контура;

 – резонансная частота контура;

 – резонансная частота собственных затухающих колебаний контура;

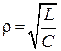 – критическое сопротивление контура;

 – характеристическое сопротивление контура.

Замечание 2: случай а) – апериодический режим работы контура, б) – критический режим работы контура, в) – колебательный режим работы.

Замечание 3:

Декремент затухания

.

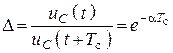Логический декремент

, где  – период собственных затуханий.

Включение R, L, C последовательного контура на источник синусоидального напряжения (рис. 98)

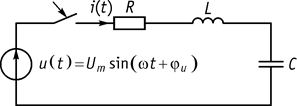
Рис. 98

Цель: определить ток в цепи и напряжение на элементах.

Алгоритм: Повторяем пункты 1-7 текста при включении  контура на источник постоянного напряжения.

8. Определяем принужденную составляющую напряжения на емкости (частное решение)

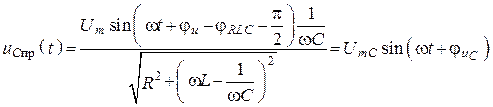, где ; ; .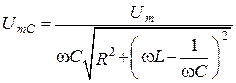

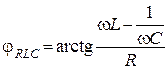Корни характеристического уравнения могут быть вида а) вещественные и разные;

б) вещественные и кратные;

в) комплексно-сопряженные.

Рассмотрим случай комплексно-сопряженных корней.

9. Запишем решение

.

10. Используя независимые начальные условия

, найдем первое уравнение для определения постоянных интегрирования

 – первое уравнение.

11. Для определения второго уравнения используем независимые начальные условия для тока в индуктивности

.

Чтобы воспользоваться этим условием, необходимо найти значение тока в индуктивности

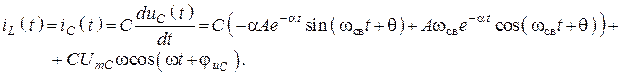
Замечание: при определении  учтем, что контур обладает большой добротностью – это значит, что

, тогда

.

Полагая , имеем

 – второе уравнение.

12. Решаем систему из двух уравнений

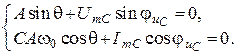
Получаем постоянные интегрирования

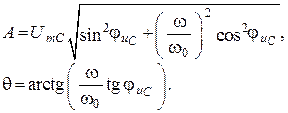
13. Зная постоянные интегрирования, записываем решение

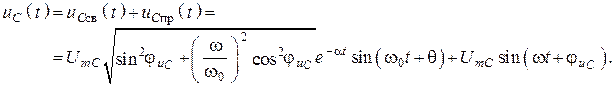
14. Зная , определяем

,

.

Анализ:

1. , . В цепи возможно сверхнапряжение

.

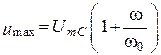2. , . В цепи возможны сверхтоки

.

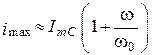3. . В цепи наблюдается явление изохронизма.

При этом ток и напряжение плавно возрастает (рис. 99, а) в соответствии с выражениями вида:

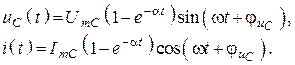
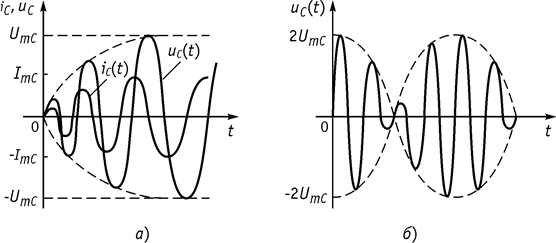
Рис. 99

4. , . В этом случае в цепи наступает явление биений (рис. 99, б).

Выражение для :

.

Переходные процессы в разветвленных цепях второго порядка

Рассмотрим схему, приведенную на рисунке 100.

Цель: определить ток в ветвях и напряжение на элементах.

Мы определяем только !

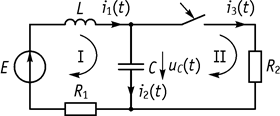
Рис. 100

Алгоритм:

1. При  определяем ток в ветвях, и напряжение на индуктивности

.

2. Находим независимые начальные условия, используя законы коммутации

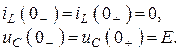
3. Записываем ЗНК и ЗТК для мгновенных значений

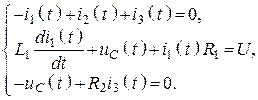
Данную систему уравнений, выбрав в качестве независимых переменных либо , либо , можно свести к одному дифференциальному уравнению второго порядка и решить также как раньше, но можно решить непосредственно данную систему уравнений.

4. Найдем характеристическое уравнение цепи, для этого заменим в уравнениях ЗНК и ЗТК операцию интегрирования на , а операцию дифференцирования на p.

Получим систему уравнений:

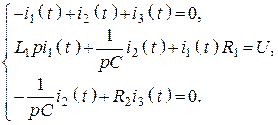
5. Составляем определитель системы и приравниваем его к 0.

Получаем характеристическое уравнение:

.

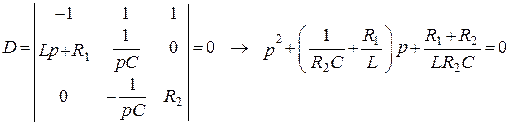6. Находим корни характеристического уравнения

.

Корни могут быть:

а) вещественными и разными;

б) вещественными и кратными;

в) комплексно-сопряженными.

Рассмотрим случай вещественных и разных корней.

7. Находим общее решение

.

8. Найдем частное решение

.

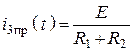9. Зная общее и частное решение, запишем решение

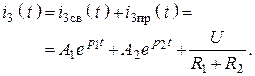
10. Для определения постоянных интегрирования  и  необходимо составить два уравнения.

1-е уравнение получим из  при

.

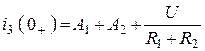2-е уравнение находим, продифференцировав ЗНК и ЗТК, но предварительно продифференцируем решение по времени

и приравняв , найдем

.

Чтобы получить 1-е и 2-е уравнения в окончательном виде необходимо найти  и .

Эти начальные условия определим из системы уравнений ЗТК (ЗНК) при  и из системы продифференцированных уравнений по времени