Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 3

Катушка, к зажимам которой подключается источник энергии, называется первичной, а катушка, к зажимам которой подключается нагрузка, называется вторичной.

Воздушный трансформатор

Электрическая схема воздушного трансформатора изображена на рисунке 66.

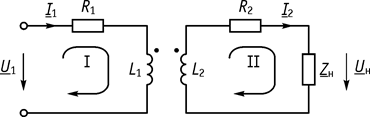
Рис. 66

Цель анализа: определение токов , определение сопротивлений, схем замещений, вносимых сопротивлений и некоторых свойств.

Анализ:

1. Выделяем контуры, задаем обход контуров.

2. Записываем ЗНК для контуров

I. ,

II. .

3. Решаем уравнения и определяем токи

,

,

.

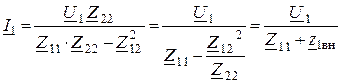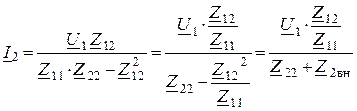4. Сопротивление ветвей

,

.

5. Вносимое сопротивление

.

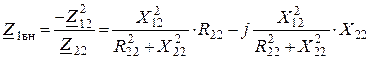Пояснение:

,

.

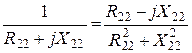 – вносимое сопротивление в I контур, за счет индуктивной связи.

 – вносимое сопротивление во второй контур, за счет индуктивной связи

.

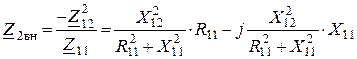6. Одноконтурные схемы замещения, основываются на уравнениях

; 

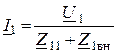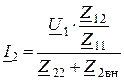
и приведены на рисунке 67.

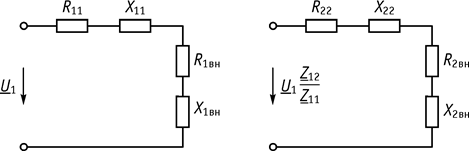
Рис. 67

7. Двухконтурная схема замещения получается при объединении одноименных зажимов воздушного трансформатора при развязке индуктивно связных катушек (рис. 68).

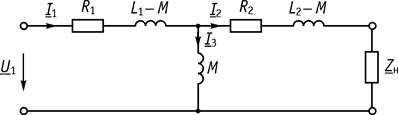
Рис. 68

Замечание 1: Эта схема (рис. 68) справедлива, если:

и практически невыполнима, если

Поэтому на практике используют приведенные схемы замещения.

8. Коэффициент замещения трансформации

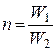, где  – количество витков 1 и 2 катушки.

9. Входное сопротивление трансформатора

.

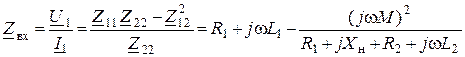Идеальный трансформатор – трансформатор, у которого:

а) потери = 0 ();

б) индуктивность = ();

в) взаимная индукция =();

г) .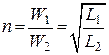

Трансформатор сопротивлений

Трансформатор сопротивлений – идеальный трансформатор, преобразующий сопротивление нагрузки. Идеальный трансформатор включен между источником энергии и нагрузки, преобразует сопротивление нагрузки пропорционально квадрату коэффициента трансформации без изменения угла (рис. 69).

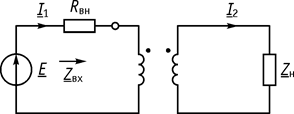
Рис. 69

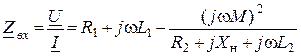
Если , тогда

,

.

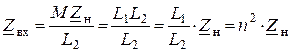Используются для развязки по постоянному току, для согласования сопротивления с генератором.

Трансформатор тока – идеальный трансформатор, имеющий сопротивление нагрузки = 0.

; .

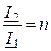Трансформатор напряжения – реализуется на основе идеального трансформатора, у которого .

;  .

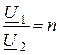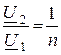Частотные характеристики линейных цепей

Комплексные передаточные функции (КПФ)

Комплексные передаточные функции – отношение комплексной амплитуды реакции цепи к комплексной амплитуде воздействия, в зависимости от вида воздействия и вида реакции различают:

1. КПФ по напряжению

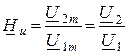 или 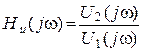, величина безразмерная.

 – комплексное действующее значение напряжения, комплексные амплитуды воздействия и реакции.

2. КПФ по току

,  

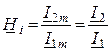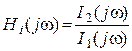
– отношение выходного тока к входному.

 – комплексное действующее значение тока, комплексные амплитуды воздействия и реакции.

3. КПФ сопротивления

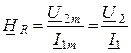  или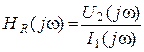 

– отношение комплексного выходного напряжения к входному току.

4. КПФ проводимости

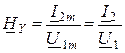  или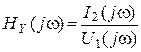   

(единицы измерения сименсы).

Кроме КПФ, рассмотренных выше, еще различают комплексные входные функции:

1. Комплексное входное сопротивление

,  .

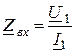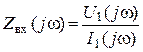2. Комплексная входная проводимость

,  .

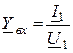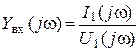КПФ можно представить в а) алгебраической форме:

;

б) показательной форме:

;

в) тригонометрической:

– амплитудно-частотная характеристика цепи;

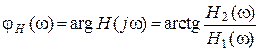
– фазочастотная характеристика цепи.

Эти понятия широко используются на практике и являются фундаментальными.

Годограф передаточной функции

Это некоторая кривая,  вычерчиваемая вектором  на комплексной плоскости , при изменении частоты от 0 до .

Пояснения: пусть имеется схема, приведенная на рисунке 70, а.

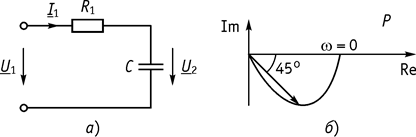
Рис. 70

Передаточная функция этой цепи:

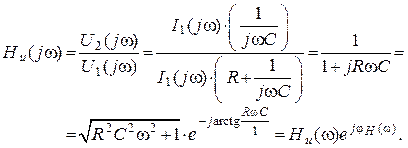
Годограф передаточной функции приведен на рисунке 70, б.

Логарифмическая АЧХ

,  [Дб].

Используется в том случае, когда  изменяется в очень широких пределах при изменении частоты .

Замечание: для активных цепей (усилители),  показывает логарифмическое усиление, для пассивных цепей вводят понятие ослабление цепи:

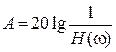, [Дб].

Резонансные цепи – электрические цепи, в которых могут возникать явления резонанса напряжения или тока.

Резонанс – такой режим работы пассивной цепи, содержащей , при котором реактивное сопротивление (реактивная проводимость) = 0.