Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 16

Получим, если в уравнение  пункта б) вместо  и  подставим их выражения в показательной форме

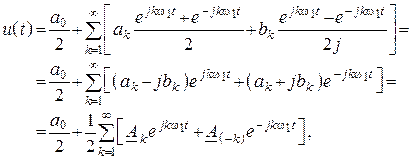
где ; .

Перейдем от 1 до  к –¥ до ¥, внесем в под знак суммы , тогда получим комплексную форму ряда Фурье

.

.

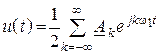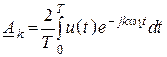Анализ переходного процесса при воздействии периодического негармонического сигнала

Пусть на вход цепи (рис. 119, а) подается функция, представленная на рисунке 119, б (периодические последовательные импульсы).

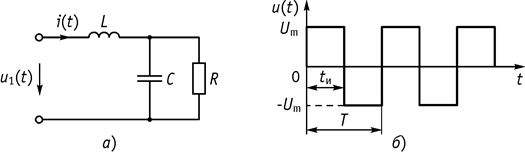
Рис. 119

Цель: необходимо определить ток  в сопротивлении .

Алгоритм:

1. Представляем входное воздействие в виде ряда Фурье, при этом заметим, что поскольку входная функция симметрична относительно начальных координат, то в ряде Фурье не будет четной гармоники (т.е. нет синуса). Поскольку входная функция имеет разные знаки на периоде, то среднее значение на периоде равно нулю

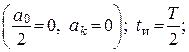
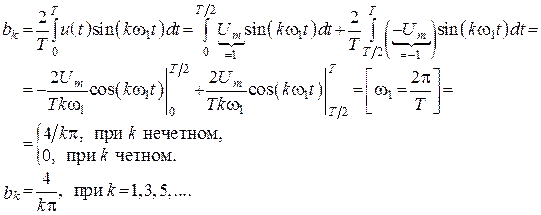
2. Найдем

.

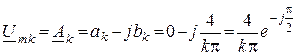3. Запишем ряд Фурье для входного сигнала

.

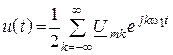4. Определим комплексную амплитуду входного тока цепи

.

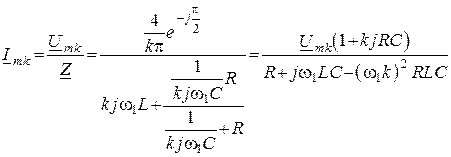5. Найдем комплексную амплитуду через по формуле разброса

.

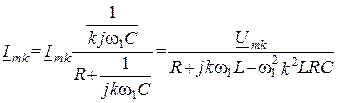6. Зная комплексную амплитуду тока, найдем мгновенное значение тока

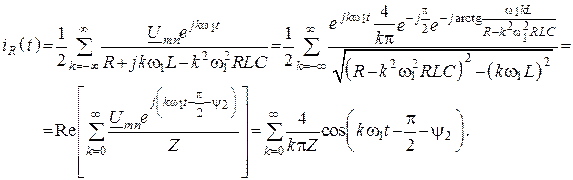
Частотный метод анализа. Ряды Фурье наиболее распространенных сигналов

1. Последовательность прямоугольных импульсов (рис. 120).

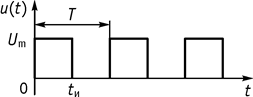
Рис. 120

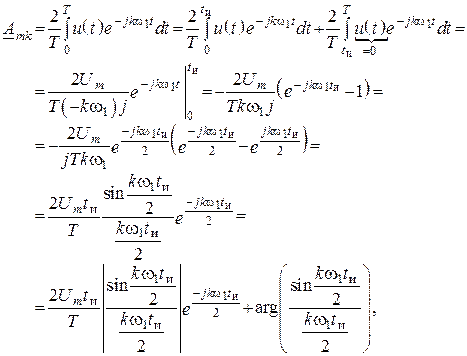
где 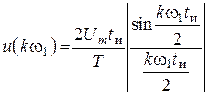 – амплитудный спектр сигнала;

 – фазовый спектр.

Видно, что амплитудный и фазовый спектры – дискретные спектры  последовательность прямоугольных импульсов имеет дискретный амплитудный и фазовый спектры.

2. Построим амплитудный и фазовый спектры для различных скважностей

.

а) Период ,  (рис. 121, а).

б) Период ,  (рис. 121, б).

в) Период ,  (рис. 121, в).

Рис. 121

Амплитудный и фазовый спектры для случая а) приведены на рисунке 122, а, для случая б) – на рисунке 122, б, для случая в) – на рисунке 122, в.

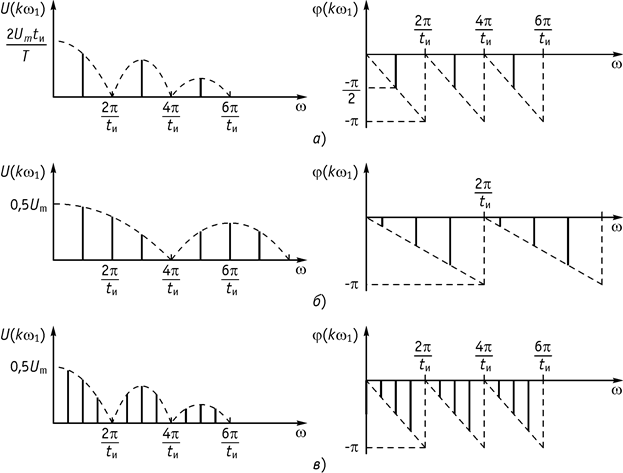
Рис. 122

Выводы:

1. Огибающая амплитудного спектра соответствует функции .

2. Частоты, на которых амплитудный спектр равен нулю, равны  k = = 1, 2, 3, ….

3. Количество составляющих между нулями равно .

4. Расстояние между гармоническими составляющими  .

5. При и увеличении (уменьшении)  расстояние между гармоническими составляющими остается постоянным, а расстояние между нулями уменьшается (увеличивается).

6. При  и увеличении (уменьшении) периода T расстояние между нулями остается постоянным, а между составляющими уменьшается (увеличивается).

Действующее, среднее значения тока и напряжения за период

Действующее значение тока

.

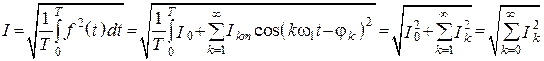Действующее значение напряжения

.

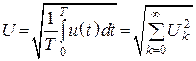Среднее значение тока за период

.

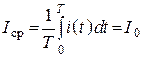Среднее значение напряжения за период

.

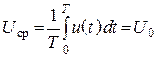Абсолютное среднее значение тока за период

.

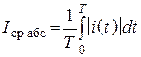Абсолютное среднее значение напряжения за период

.

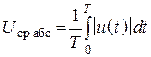Активная, реактивная и полная мощность цепи при периодическом негармоническом сигнале

1. Активная мощность

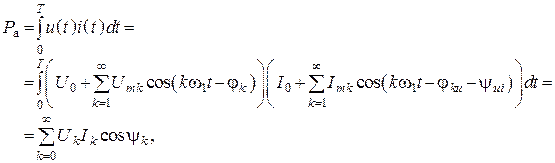
где  – угол между током и напряжением k-ой гармоники/

2. Реактивная мощность

.

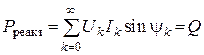3. Полная мощность

.

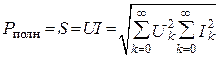Замечание: .

4. Мощность искажения

.

5. Коэффициент мощности

.

6. Коэффициент формы сигнала

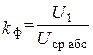 (для синусоиды ).

7. Коэффициент искажения

 (для синусоиды ), где  – амплитуда первой гармоники.

8. Коэффициент амплитуды

 (для синусоиды ).

9. Коэффициент гармоник

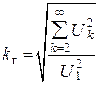 (для синусоиды ).

Частотный (спектральный) метод анализа переходных процессов в линейных электрических цепях при негармоническом непериодическом воздействии

Основан на преобразовании Фурье, если функция  удовлетворяет:

а) условию абсолютной интегрируемости

;

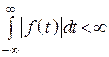б) условию ограниченного роста

, где  – некоторые числа, то функция  может быть преобразована по Фурье

Прямое преобразование Фурье

Комплексный спектр сигнала, комплексная спектральная плоскость

.

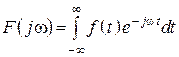Обратное преобразование Фурье

.

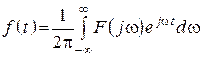Замечание: спектр  можно представить в следующих видах:

, где  и  – действительная и мнимая часть соответственно;  – спектральная плотность амплитуд, (амплитудный спектр), функция четная;  – фазовый спектр, функция нечетная

, .

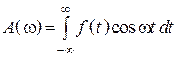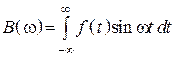Физический смысл обратного преобразования Фурье

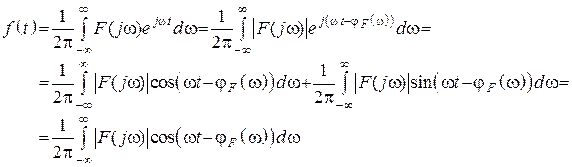
или

 –

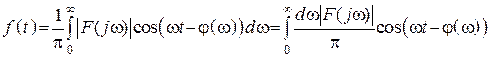– сигнал представляется в виде суммы бесконечного количества гармонических составляющих с бесконечно малыми амплитудами