Замечание 2: ток в индуктивном элементе и напряжение на емкостном элементе не может изменяться скачком.
Замечание 3: есть ситуации, когда 1 и 2 законы не выполняются, например: при переключении индуктивного элемента на другой индуктивный элемент (рис. 94, а), емкостного элемента на другой емкостной элемент (рис. 94, б). В этих случаях используют вместо законов коммутации: 1. Закон постоянства суммарного потокосцепления (на принципе непрерывности суммарного потокосцепления). 2. Закон постоянства заряда (на принципе непрерывности суммарного заряда). В этом случае допускают возможность скачкообразного изменения тока в индуктивности и напряжения на емкости.
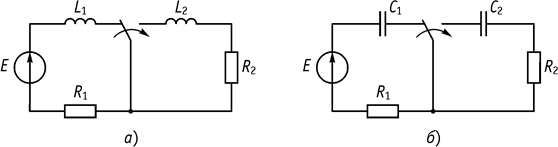
Рис. 94
При решении задачи переходных процессов используют начальные условия решения задачи. Различают начальные условия: зависимые и независимые, нулевые и ненулевые.
Независимые начальные условия: основаны на 1-м и 2-м законах коммутации и представляют собой
значения токов в индуктивностях и напряжения на емкостных элементах в момент
времени t = 0+ (
). Бывают нулевыми 
и ненулевыми 
.
Зависимые начальные условия: представляют собой значения напряжений на резистивных и индуктивных элементах, и значения токов в резистивных и емкостных элементах в момент времени t = 0+. Получаются из ЗТК и ЗНК. Бывают нулевыми и ненулевыми.
Классический метод анализа
Классический метод анализа основан на составлении интегро-дифференциальных уравнений, как правило, по закону Кирхгофа относительно выбранных независимых переменных, в качестве которых берутся ток в индуктивности или напряжение на емкости.
Интегро-дифференциальные уравнения с помощью преобразований обычно сводятся к одному дифференциальному уравнению n-го порядка вида
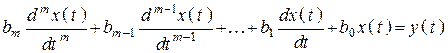
– линейное дифференциальное
уравнение (неоднородное) n-го порядка, где 
– некоторые коэффициенты,
обусловленные параметрами схемы; 
– реакция и
воздействие цепи соответственно.
Порядок уравнения n определяется количеством реактивных элементов.
Решение линейного неоднородного дифференциального уравнения состоит из двух решений:
I. Общего решения: 
, которое получается при решении однородного
уравнения вида
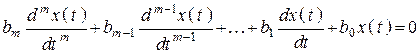, которое представляет собой
сумму экспоненциальных функций вида 
.
Вид суммы этих функций зависит от типа корней
характеристического уравнения, которое получается подстановкой в однородное
дифференциальное уравнение вместо реакции x(t) , и с последующим сокращением
одинаковых сомножителей. Уравнение имеет вид
– характеристическое уравнение m-го порядка.
При определении корней характеристического уравнения возможны следующие виды корней:
1) Корни вещественные и разные
, где р1, …, рm – корни характеристического уравнения.
2) Корни вещественные и кратные
, где р – корень; m – кратность.
3) Корни комплексно-сопряженные (как правило, попарно-кратные)
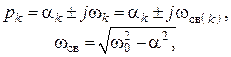
где w0 – резонансная частота.
Решение имеет вид
,
4) Имеются все корни 1, 2, 3 случаев.
II. Частное решение: определяется любым методом анализа цепи в установившемся (принужденном) режиме работы при t = ¥.
Замечание: общее решение характеризует свободные процессы, происходящие
в электрической цепи при отсутствии воздействия y(t). Частное решение 
характеризует
принужденные процессы при наличии воздействия y(t) при t = ¥.
Общий алгоритм анализа переходных процессов
1. Выбираем независимые переменные, iL(t) и iС(t).
2. Определяем начальные условия, глядя на схему и используя законы коммутации.
3. Методом законов Кирхгофа составляем систему интегро-дифференциальных уравнений относительно выбранных переменных.
4. Интегро-дифференциальную систему сводим к одному дифференциальному уравнению относительно одной переменной (хотя можно решать систему).
5. Ищем решение дифференциального уравнения в виде суммы 2-х решений
.
6. Определяем характеристическое уравнение дифференциального уравнения.
7. Определяем корни характеристического уравнения.
8. Зная корни, записываем общее решение
.
9. Определяем частное решение любым известным методом, используя схему при t = ¥ (установившийся принужденный режим).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.