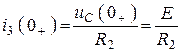 ,
,
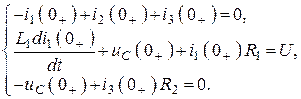
Продифференцируем ЗНК и ЗТК по времени и приравняем к 0 время
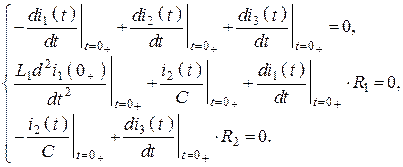
Решая системы совместно
(непродифференцированную и продифференцированную), используем независимые
начальные условия, определяем зависимые начальные условия, решаем систему двух
уравнений и определяем ![]() .
.
Зная постоянные интегрирования ![]() ,
записываем окончательное решение
,
записываем окончательное решение
Замечание1: порядок
дифференциального уравнения определяется количеством реактивности, т.е. ![]() , где
, где ![]() –
количество индуктивностей,
–
количество индуктивностей, ![]() – количество
емкостей.
– количество
емкостей.
Однако есть электрические цепи, в которых порядок дифференцирования уравнения меньше количества реактивности. Это может быть обусловлено:
а) наличием особых ![]() -контуров
(рис. 101, а) и особых
-контуров
(рис. 101, а) и особых ![]() -сечений
(рис. 101, б);
-сечений
(рис. 101, б);
б) конфигурации схемы (рис. 101, в).
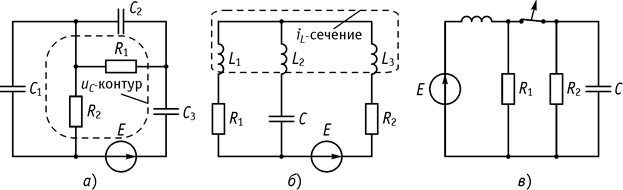
Рис. 101
Операторный метод анализа переходных процессов
Базируется на преобразованиях Лапласа, которые позволяют систему дифференциальных уравнений свести к системе алгебраических уравнений и найти требуемые неизвестные обычным аппаратом алгебры.
Различают:
а) Прямое преобразование Лапласа
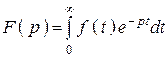 .
.
б) Обратное преобразование Лапласа
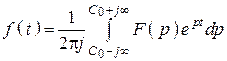 .
.
Преобразования Лапласа позволяют переходить от действительной переменной t к комплексной p и обратно от p к t.
Виды записи преобразования Лапласа
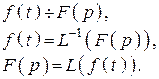
Замечание: по Лапласу могут быть преобразованы те функции, которые удовлетворяют следующим требованиям:
1. ![]() при
при ![]() ;
; ![]() ,
при t < 0.
,
при t < 0.
2. ![]() , где М, С
– некоторые коэффициенты;
, где М, С
– некоторые коэффициенты; ![]() – показатель роста
функции, т. е функция не должна быть бесконечна.
– показатель роста
функции, т. е функция не должна быть бесконечна.
Основные свойства преобразования Лапласа
1. Линейность
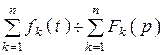 .
.
2. Дифференцирование оригинала а) начальные условия нулевые;
б) начальные условия не нулевые.
Для:
а) ![]() ;
;
б) ![]() ;
;
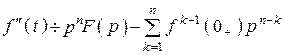 .
.
3. Интегрирование оригинала
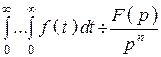 .
.
4. Изменение масштаба действительного переменного
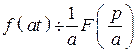 .
.
5. Смещение в области действительного переменного (теорема запаздывания)
![]() .
.
6. Смещение в области комплексного переменного
![]() .
.
7. Дифференцирование оригинала по параметру
![]() .
.
8. Интегрирование оригинала по параметру
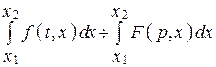 .
.
9. Умножение изображения имеет свертку оригинала
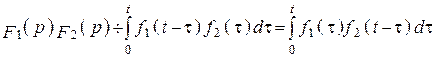 .
.
10. Дифференциальное изображение
![]() .
.
11. Интеграл от изображения
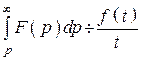 .
.
12. Умножение оригинала на синусоиду
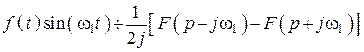 .
.
13. Умножение оригинала на косинус
![]() .
.
14. Предельное сопротивление а) ![]() ;
;
б) ![]() .
.
Замечание к б): функция ![]() не должна иметь полюсов на мнимой оси
и в правой полуплоскости комплексной плоскости p.
не должна иметь полюсов на мнимой оси
и в правой полуплоскости комплексной плоскости p.
15. Теорема единственности.
Если оригинал ![]() имеет
изображение
имеет
изображение ![]() , то
, то ![]() –
единственное. Если изображение
–
единственное. Если изображение ![]() имеет оригинал
имеет оригинал ![]() , то оригинал – единственен.
, то оригинал – единственен.
Методы определения оригинала по изображению
Это методы решения интеграла – обратного преобразования Лапласа
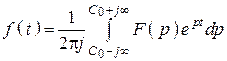 .
.
1. Методы, основанные на теореме вычетов. Решение при этом зависит от вида полюсов
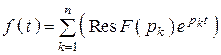 , где
, где ![]() –
полюс функции вида
–
полюс функции вида
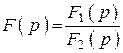 .
.
Полюс – это корень полинома знаменателя функции
![]() полюсы,
полюсы,
![]() нули.
нули.
а) Простые полюсы (корни ![]() вещественные
и разные)
вещественные
и разные)
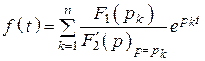 .
.
б) Полюсы кратные (корни вещественные и одинаковые)
Ряд корней имеют кратность ![]() , в
общем случае
, в
общем случае ![]() – кратность k-го
корня.
– кратность k-го
корня.
Решение имеет вид:
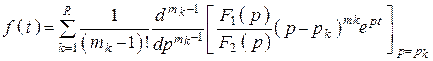 , где R – количество кратностей корней.
, где R – количество кратностей корней.
в) Полюсы попарно комплексно-сопряженные
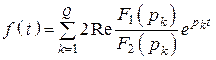 , где Q – количество пар полюсов.
, где Q – количество пар полюсов.
2. Основан на разложении
функции ![]() на простые дроби вида:
на простые дроби вида:
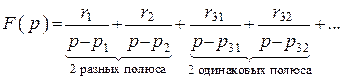 , где
, где ![]() –
вычеты функции
–
вычеты функции ![]() в соответствующих полюсах.
Они могут быть определены не через вычеты, а по методу неопределенных коэффициентов.
в соответствующих полюсах.
Они могут быть определены не через вычеты, а по методу неопределенных коэффициентов.
Замечание 1: если имеется
изображение, и необходимо найти значение функции в момент времени ![]() или
или ![]() , то
необходимо воспользоваться предельными соотношениями.
, то
необходимо воспользоваться предельными соотношениями.
![]() Замечание 2: при разложении полинома
Замечание 2: при разложении полинома ![]() на простые дроби
оригинал находится в виде
на простые дроби
оригинал находится в виде
![]() .
.
Замечание 3: если полином ![]() имеет нулевой полюс, тогда оригинал
определяется по формуле
имеет нулевой полюс, тогда оригинал
определяется по формуле
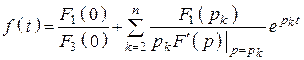 ,
,
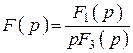 .
.
Изображение наиболее часто встречающихся функций
1. Единичная (ступенчатая) (рис. 102, а)
![]()

Рис. 102
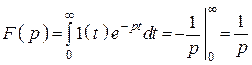 .
.
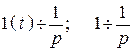 .
.
2. Единичная импульсная функция (функция Дирака – дельта функция) (рис. 102, б)
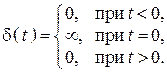
![]() – физически нереализуемая
функция (математическая абстракция), играет важную роль при теоретических
исследованиях.
– физически нереализуемая
функция (математическая абстракция), играет важную роль при теоретических
исследованиях.
![]() может быть получена
из предельного соотношения единичного импульса площадью равной единице (рис.
102, в).
может быть получена
из предельного соотношения единичного импульса площадью равной единице (рис.
102, в).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.