Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 13

Единичный импульс может быть получен как разность двух импульсов (рис. 102, в).

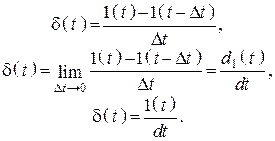
Свойства d-функции

1. .

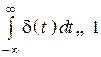2. Фильтрующее свойство

.

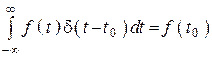Изображение d-функции можно определить, найдя изображение двух ступенчатых функций и перейдя к пределу при

.

3. Экспоненциальная функция

,

.

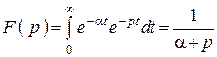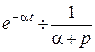4. .

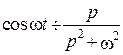5. .

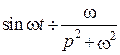Изображение пассивных элементов цепи

1. Сопротивление (рис. 103).

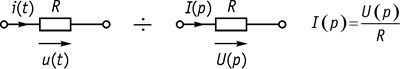
Рис. 103

2. Емкость (рис. 104).

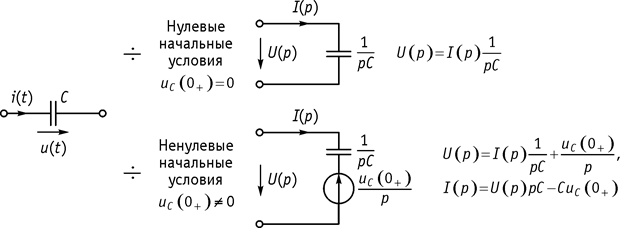
Рис. 104

3. Индуктивность (рис. 105).

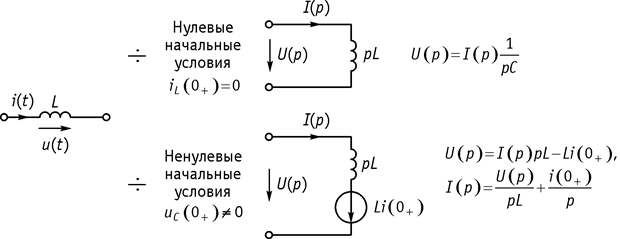
Рис. 105

Изображение источников

1. Источник постоянного напряжения (рис. 106, а).

2. Источник постоянного тока (рис. 106, б).

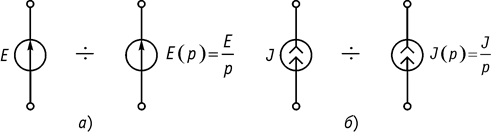
Рис. 106

3. Источник переменного напряжения (рис. 107).

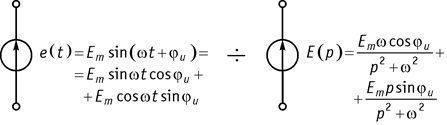
Рис. 107

4. Источник переменного тока (рис. 108).

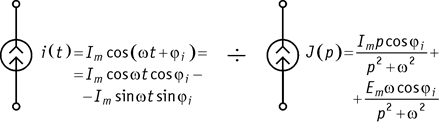
Рис. 108

Законы Ома и Кирхгофа в операторной форме

Рассмотрим законы Ома и Кирхгофа на примере схемы, изображенной на рисунке 109, а. Операторная схема замещения приведена на рисунке 109, б.

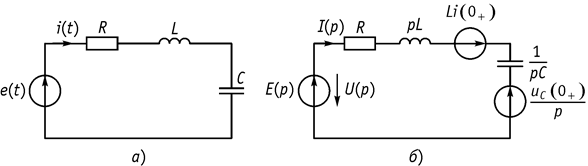
Рис. 109

Начальные условия ненулевые, т.о.

ЗНК

.

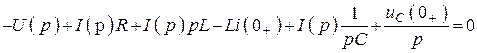Закон Ома

.

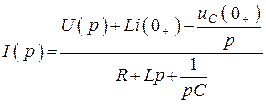Сопротивление в операторной форме

.

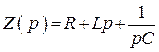Операторный метод анализа переходных процессов в цепях первого порядка

Переключение цепи RC и RL с источника постоянного напряжения  на источник постоянного напряжения .

Необходимо найти  ток  и напряжение U. Анализ переходного процесса приведен в таблице 4.

Таблица 4

Цепь RС	Цепь RL
1. Определяем ток и напряжение при
2. Находим независимые начальные условия
3. Нарисуем схему в операторной форме, учитывая начальные условия при
4. Определяем операторный ток
5. Записываем характеристическое уравнение, для этого приравниваем операторное сопротивление к 0
6. Находим корни характеристического уравнения (полюсы функции)
7. Зная корни, найдем оригинал тока
,	,
8. Зная ток, найдем напряжение

Операторный метод анализа переходных процессов в разветвленных цепях

Рассмотрим схему, приведенную на рисунке 110.

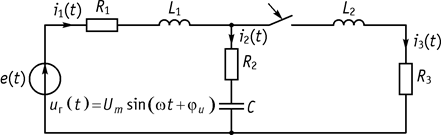
Рис. 110

Алгоритм

1. Определяем токи в ветвях

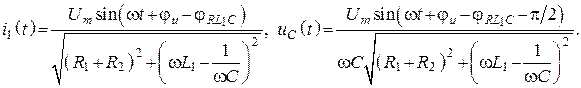
2. Определим независимые начальные условия

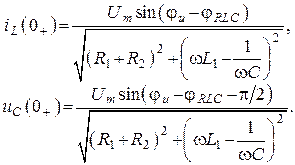
3. Нарисуем операторную схему с учетом начальных условий. Полученная операторная схема приведена на рисунке 111.

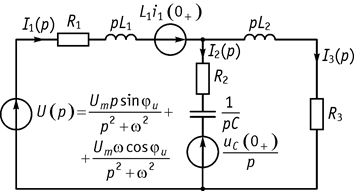
Рис. 111

4. ЗТК и ЗНК

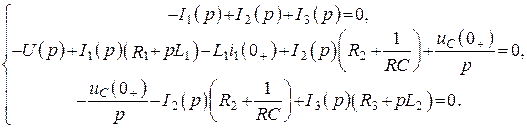
5. Используя четвертый пункт, определяем ток

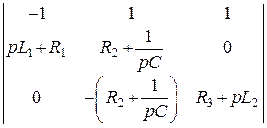 – главный определитель.

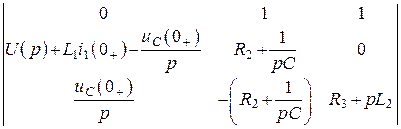 – для .

6. Определяем характеристическое уравнение, для этого приравниваем главный определитель к 0.

7. Найдем корни характеристического уравнения а) вещественные и разные (полюсы вещественные);

б) вещественные и одинаковые (кратные полюсы);

в) комплексно-сопряженные.

8. В зависимости от корней, оригиналы токов определяются по выше приведенным формулам.

Операторные передаточные функции

1. По напряжению

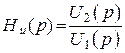 – (величина безразмерная).

2. По току

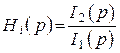 – (безразмерная величина).

3. Операторное передаточное сопротивление

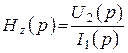, (Ом).

4. Операторная передаточная проводимость

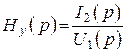, (См).

Представление операторной передаточной функции:

1. В виде дробной рациональной функции

.

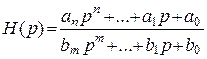2. В виде отношения произведений нулей и полюсов функции

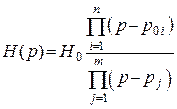, где  – соответственно нули и полюсы функции .

Свойства операторной передаточной функции:

1. Является дробно рациональной функцией.

2. .

3. Нули передаточной функции для физически существующей пассивной цепи могут находиться как в правой, так и в левой полуплоскостях комплексной плоскости p.

4. Полюсы функции пассивной цепи находятся в левой полуплоскости комплексной плоскости p (это указывает на затухание происходящих процессов).

Связь операторной передаточной функции и комплексной передаточной функции

Комплексную передаточную функцию  можно получить из операторной передаточной функции , заменив в  p на jw. Получим:

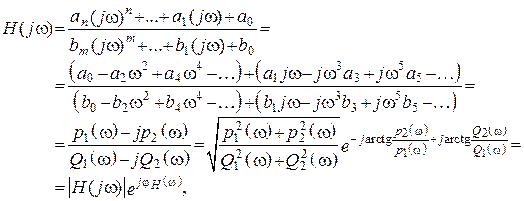
где  – АЧХ,   – ФЧХ.