Это уравнение эллипса. Т.е. поверхность взаимодействия колеса и рельса при неподвижном колесе имеет форму эллипса. Величина эллипса зависит от:
- величины нагрузки колеса на рельс;
- модуля упругости материалов колеса и рельса;
- радиусов поверхностей взаимодействия колеса и рельса:
Распределение давления колеса на рельс имеет форму эллипсоида. Давление в произвольной точке эллипсоида равно:
.
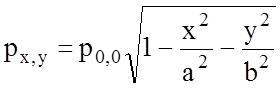В центре эллипса
(х = 0, у = 0) давление максимально и равно
.
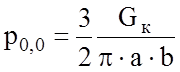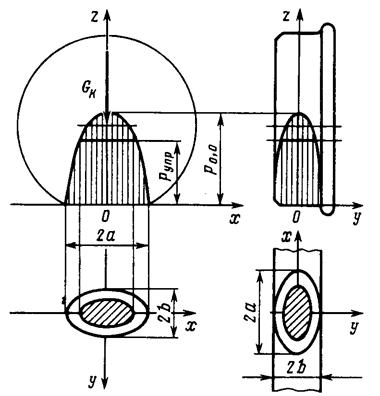
Для современных грузовых электровозов давление в центре эллипса в 1,5 раза больше среднего и у превышает предел упругости рупр колеса и рельса. Иными словами, в пределах заштрихованной площади происходят упругопластические деформации материалов колеса и рельса.
Коническое очертание поверхности катания колеса и наклон поверхности катания рельса сильно усложняют решение задачи. Приближенно считают, что опорная поверхность в этом случае также имеет форму эллипса, площадь которого составляет 400-600 мм2. Меньшие значения площади соответствуют малым диаметрам колес и малым нагрузкам на ось.
Ориентация эллипса и его размеры зависят от степени проката бандажа и износа рельса. При увеличении износа поверхность взаимодействия искажается и при изношенных бандаже и рельсе принимает форму, близкую к прямоугольнику, большая ось которого направлена поперек рельса.
4.3. Перераспределение сил взаимодействия колеса и рельса под действием вращающего момента.
|
|
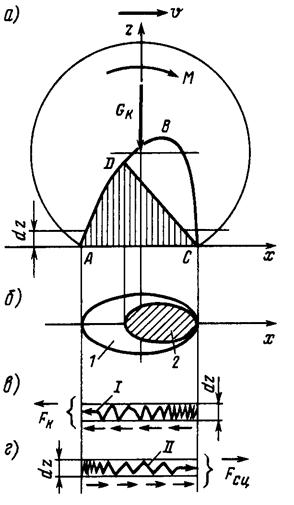
Как было условленно ранее, учитываем только упругие деформации колеса и рельса. Под действием вращающего момента колесо испытывает упругий подпор со стороны рельса, который схематично представлен равнодействующими силами F1 и F2 и условным возвышением уровня рельса в направлении движения. Вследствие этого нарушается симметрия распределения напряжений в зоне контакта.
Если представить, что при неподвижном колесе его поверхность состоит из волокон, направленных поперек профиля колеса и равномерно распределенных по поверхности, то вследствие действия сил F1 и F2 волокна, расположенные на набегающем крае колеса испытывают сжатие, а со стороны сбегающего края – растяжение. Для материала рельса – картина обратная.
Одновременно под действием вращающего момента возникает по опорной поверхности касательная сила t, равная произведению коэффициента трения m в данной точке этой поверхности на нормальное давление р. Значение m, различно по опорной поверхности и зависит от зоны, в которой находится данная точка. На опорной поверхности различают две зоны: зону качения 1, в которой коэффициент трения m = 0 и касательные силы поэтому не развиваются, и зону сцепления 2, в которой m ¹ 0 и возникают силы трения.
Процесс сцепления состоит из двух последовательных фаз. В течение
первой фазы коэффициент трения возрастает от нуля до значения, соответствующего
трению покоя: во второй фазе он остается неизменным до тex
пор, пока набегающие волокна новых частиц бандажа не вступят в контактную
площадку. Соответственно изменению произведения коэффициента трения на
нормальное давление меняется и касательная сила. Поэтому эпюра распределения
касательных сил но опорной поверхности оказывается отличной от эпюры
распределения нормальных давлений. В зоне сцепления, когда коэффициент трения
растет от нуля до максимального значения, равного коэффициенту трения покоя, а
нормальное давление изменяется по эллипсу (линия CBD),
определить закон изменения касательной силы весьма трудно. В первом
приближении, его можно принять линейным (линия CD).
Когда же коэффициент трения достигает максимального значения, касательная сила
изменяется по эллиптическому закону, соответствующему изменению нормальною
давления по опорной поверхности (линия DA). Эта
касательная сила вызывает деформации материала бандажа, которые в сбегающей
части его опорной поверхности являются деформациями растяжения.
По мере дальнейшего вращения колеса и выхода материала бандажа из опорной поверхности соприкосновения волокна его стремятся под действием сил упругости возвратиться в недеформированное состояние. Вследствие этого волокна материала бандажа перемещаются в сторону, противоположную поступательному движению колеса (в набегающем крае колеса как бы наблюдается избыток волокон, в сбегающем – как бы недостаток). Таким образом, в сбегающей зоне опорной поверхности бандажа происходит проскальзывание относительно поверхности рельса разжимающихся волокон бандажа в направлении, противоположном поступательному движению колеса. Условно оно показано стрелкой I нарисунке. В виде реакции рельса на эти относительные перемещения волокон возникает равнодействующая сил трения по опорной поверхности, направленная в обратную сторону, т.е. по направлению поступательного движения колеса (стрелка II). Она и представляет собой внешнюю для колеса силу – силу сцепления.
|
|
Рассмотрим процесс перемещения волокон колеса по опорной поверхности при повороте колеса на элементарный угол da. В случае недеформированного колеса перемещение его центра за da будет равно:
dx = dxa = R × da.
Но, т.к. волокна нашего колеса имеют перемещение относительно опорной поверхности, вызванное упругими деформациями, то:
dx = dxa – du.
Таким образом, вследствие относительных перемещений волокон бандажа и рельса, обусловленных упругостью их материалов, путь, проходимый волокнами в режиме тяги меньше пути, проходимого геометрическим центром колеса на величину упругой деформации:
du = dxa – dx.
Это явление называют упругим скольжением. В иностранной литературе оно носит название крипа (ползучести).
Из полученного выражения следует, что в режиме тяги действительный путь, проходимый колесом меньше пути, подсчитанного по угловой скорости и геометрическому радиусу (dxa < R × da) – колесо как бы проскальзывает относительно рельса. Поэтому упругое скольжение отрицательно и направлено против поступательного движения колеса. Если сделать аналогичные выкладки для режима торможения – получим обратный результат: путь, проходимый волокнами больше пути, проходимого геометрическим центром колеса на величину упругой деформации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
