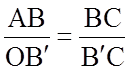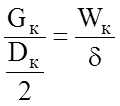;
.
Поскольку величина d, по сравнению с Dк мала (0,1¸0,2 мм), то можно приближенно записать:
;
.
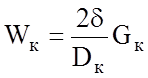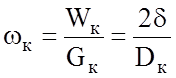Деформация пути приводит к тому, что колесо как бы гонит перед собой упругую волну изгибающегося рельса. Т.е. колесо как бы постоянно преодолевает воображаемый подъем. Исследования при проектировании и обкатке поезда TGV показали, что при скорости 380 км/ч величина этого уклона может достигать 0,37 ‰. Величина сопротивления движению от деформации пути зависит от жесткости пути (мощность верхнего строения) и нагрузки на ость.
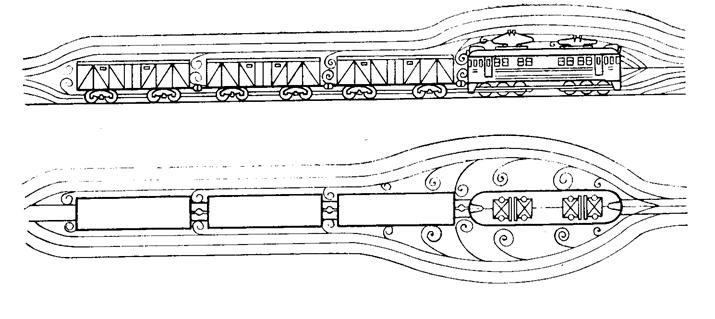
Сопротивление воздушной среды можно подразделить на:
- лобовое (обусловлено давлением набегающего потока воздуха на лобовую поверхность поезда). Зависит от формы лобовой части поезда и площади поперечного сечения;
- кормовое (обусловлено разряжением за последним вагоном). Зависит от формы хвостовой части поезда;
- межвагонное (обусловлено завихрениями воздуха между вагонами). Зависит от расстояния между вагонами. Можно уменьшить применением гибких "шторок" между вагонами (ЭР200);
- сопротивление от трения воздуха о боковые поверхности поезда;
- сопротивление от крышевого и подвагонного оборудования.
На
основании аэродинамических исследований движения тела неизменяемой формы в
воздушном потоке установлено, что сила сопротивления примерно пропорциональна
квадрату скорости и зависит от его формы. В эмпирической формуле для основного
сопротивления движению сопротивлению воздушной среды соответствует член 
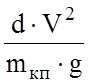. Коэффициент d
зависит от формы головного и хвостового вагона (kф),
площади его поперечного сечения (S); от состояния
поверхности поезда и его длины (Lп):
,
где kпс – коэффициент, который учитывает тип подвижного состава, состояние поверхности поезда и другие факторы;
r – плотность воздуха.
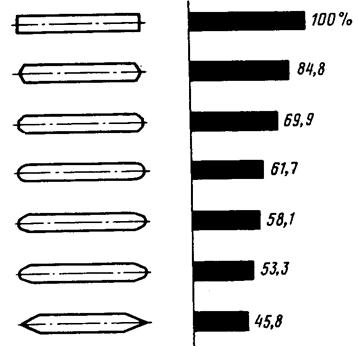
На рисунке показано изменение сопротивление движению поезда в зависимости от формы головной и хвостовой части.
3.1.1. Сопротивление движению при трогании с места.
Увеличение сопротивления движению при трогании поезда с места особенно сильно проявляется у вагонов, имеющих подшипники скольжения. Объясняется это тем, что при стоянке поезда более 20 мин происходит стекание смазки с оси колесной пары и при трогании с места возникает сухое трение. В зимних условиях при загустении смазки этот эффект проявляется еще сильнее. В настоящее время вагонов с подшипниками скольжения практически не осталось. Сопротивление моторно-осевых подшипников электровозов при трогании с места не учитывается. Поэтому актуальным является учет сопротивления движению вагонов, оборудованных роликовыми подшипниками.
В отношении сопротивления троганию вагонов, оборудованных роликовыми подшипниками, до сих пор имеются лишь разрозненные сведения, согласно которым принимают
.
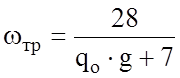3.2. Дополнительное сопротивление движению.
3.2.1. Сопротивление движению от уклонов.
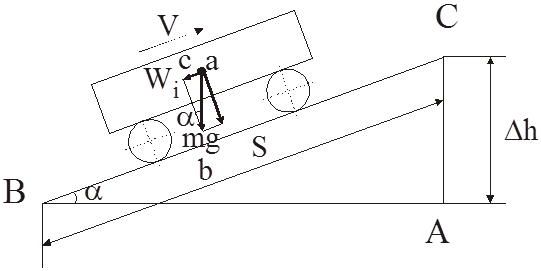Предположим,
что экипаж движется вверх по подъему с постоянной скоростью V. В этом случае на него действует сила тяжести,
направленная вертикально вниз. Выберем систему координат, одна из осей которой
направлена параллельно плоскости, в которой происходит поступательное движение
экипажа. Сделаем проекции силы тяжести на оси координат. Одна из проекций
представляет собой реакцию опоры на действие силы тяжести и для нас интереса не
представляет. Вторая проекция – это сила, направленная навстречу движению, и
является искомой силой сопротивления движению от уклона.
Wi = mg × wi = mg × sina.
Таким образом, порождением силы сопротивления движению от уклона является сила тяжести. При движении по подъему эта сила препятствует движению; при движении по спуску – способствует ему.
При рассмотрении подобных треугольников abc и АВС можно записать:
.
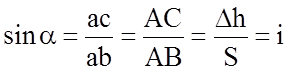Размерность удельного
сопротивления движению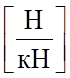 
. Эту размерность
можно интропретировать как 
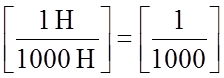– то есть
величина удельного сопротивления движению от уклона численно равна синусу угла,
характеризующего крутизну уклона в том случае, если величина возвышения пути Dh [м]
рассматривается на 1 км пути (S). То есть уклон в
1 ‰ означает возвышение пути в 1 м на 1000 м пройденного пути.
Wi = mg × i;
wi = i.
То есть удельное сопротивление от уклона численно равно величине уклона, выраженного в тысячных. При этом оно не зависит ни от скорости движения, ни от типа подвижного состава.
3.2.2. Сопротивление движению от кривых.
При прохождении кривых участков пути возникает дополнительное сопротивление движению. Можно выделить две основные причины возникновения этого сопротивления:
- проскальзывание колес из-за разницы пути, проходимого колесом, движущимся по внешней и внутренней ниткам кривой;
- повышенное трение гребня бандажа колеса, движущегося по внешней нитке кривой вследствие действия центробежной силы.
Из-за сложности учета факторов, влияющих на этот вид сопротивления движению, для его учета обычно пользуются эмпирической формулой, которая учитывает только радиус кривой:
,
где Ккр – коэффициент, зависящий от типа подвижного состава и радиуса кривой.
В случае представления поезда не материальной точкой, а распределенной массой при входе и выходе из кривой следует учитывать, что в кривой находится только часть поезда:
,
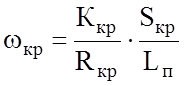где Sкр – длина кривой;
Lп – длина поезда.
В том случае, если характеристика кривой представлена в виде угла поворота пути в кривой aкр, то, учитывая, что
,
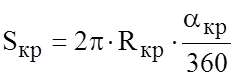можно записать, выразив радиус кривой из приведенного выражения:
.
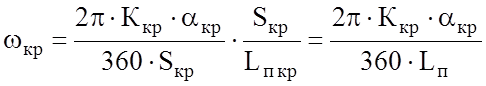Как говорилось выше одной из причин, вызывающей увеличение сопротивление движению в кривой, является непогашенное ускорение. Для одиночного экипажа можно записать
,
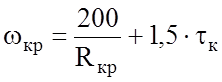где tк – непогашенное ускорение в кривой.
.
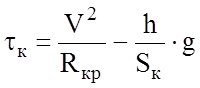Здесь h – возвышение наружного рельса в кривой;
Sк – расстояние между кругами катания.
Можно записать:
,
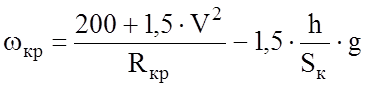3.2.3. Сопротивление движению в тоннелях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.