- изменение плана и профиля пути.
4. Образование и реализация силы тяги.
4.1. Образование силы тяги при точечном контакте колеса и рельса.
Вспомним уравнение движения поезда в общем виде без учета взаимного перемещения вагонов внутри поезда:
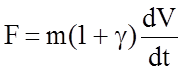 .
.
здесь F – равнодействующая сил, действующих на поезд.
В общем случае равнодействующая сил, действующих на поезд, складывается из силы тяги локомотива, силы сопротивления движению и тормозной силы поезда:
![]() .
.
Рассмотрим образование силы тяги локомотива. Рассмотрим образование силы тяги при абсолютно жестком колесе и рельсе, т.е. ни колесо, ни рельс при взаимодействии не испытывают деформацию и, как следствие этого, контакт колеса и рельса является точечным.
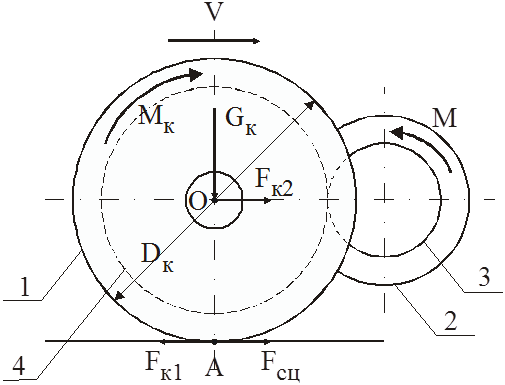 Как
известно, источником движения поезда при электрической тяге являются тяговые
двигатели электровоза. Тяговый двигатель развивает вращающий момент М,
который посредством редуктора 3-4 передает его на колесную пару 1. При этом
происходят потери. Обозначив потери на трение как Мтр, а
потери на преодоление момента инерции – Мин, можно записать
Как
известно, источником движения поезда при электрической тяге являются тяговые
двигатели электровоза. Тяговый двигатель развивает вращающий момент М,
который посредством редуктора 3-4 передает его на колесную пару 1. При этом
происходят потери. Обозначив потери на трение как Мтр, а
потери на преодоление момента инерции – Мин, можно записать
![]() .
.
Как известно из курса физики, момент на ободе колеса
можно заменить парой сил ![]() с плечом Dк/2. Сила
Fк1 приложена в точке опоры колеса на
рельс (точка А) и направлена в противоположную сторону по отношению к направлению
движения. Эта сила стремиться переместить точку А против движения колеса. Под
воздействием силы давления колеса на рельс Gк,
как реакция рельса на силу Fк1, в
точке контакта возникает внешняя по отношению к колесу сила Fсц, которая равна по модулю силе Fк1 и направлена противоположно последней. Эта
сила препятствует перемещению точки А. Точка А оказывается как бы
зафиксированной относительно рельса и называется мгновенным центром поворота.
с плечом Dк/2. Сила
Fк1 приложена в точке опоры колеса на
рельс (точка А) и направлена в противоположную сторону по отношению к направлению
движения. Эта сила стремиться переместить точку А против движения колеса. Под
воздействием силы давления колеса на рельс Gк,
как реакция рельса на силу Fк1, в
точке контакта возникает внешняя по отношению к колесу сила Fсц, которая равна по модулю силе Fк1 и направлена противоположно последней. Эта
сила препятствует перемещению точки А. Точка А оказывается как бы
зафиксированной относительно рельса и называется мгновенным центром поворота.
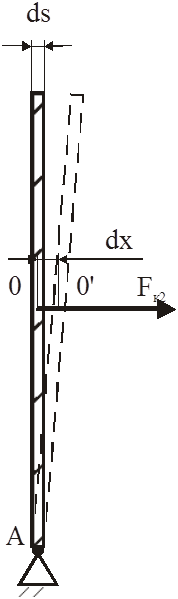 Сила Fк2, приложенная к точке 0 стремиться переместить
ее в направлении движения. Для пояснения рассмотрим мгновенную схему. Возьмем
бесконечно малое сечение колеса ds в
вертикальной плоскости. При этом сечение можно представить как стержень с
шарнирно закрепленным концом в точке А. сила
Fк2, приложенная к точке 0 стремиться
повернуть стержень по часовой стрелке. Точка 0 перемещается на бесконечно малое
расстояние dx. За счет конечности диаметра
колеса точка А за тот же промежуток времени переместится относительно рельса,
т.е. возникнет новый мгновенный центр поворота. Следовательно, в следующий
момент времени необходимо рассматривать новое сечение с новым центром поворота.
Сила Fк2, приложенная к точке 0 стремиться переместить
ее в направлении движения. Для пояснения рассмотрим мгновенную схему. Возьмем
бесконечно малое сечение колеса ds в
вертикальной плоскости. При этом сечение можно представить как стержень с
шарнирно закрепленным концом в точке А. сила
Fк2, приложенная к точке 0 стремиться
повернуть стержень по часовой стрелке. Точка 0 перемещается на бесконечно малое
расстояние dx. За счет конечности диаметра
колеса точка А за тот же промежуток времени переместится относительно рельса,
т.е. возникнет новый мгновенный центр поворота. Следовательно, в следующий
момент времени необходимо рассматривать новое сечение с новым центром поворота.
Таким образом, вследствие действия внешней силы Fсц в точке опоры колеса на рельс, мгновенный центр поворота непрерывно перемещается вдоль рельса, а геометрический центр колеса получает поступательную скорость V, которая является скоростью движения электровоза.
Следовательно, внешняя сила Fсц является той силой, благодаря которой вращающий момент ТД реализуется в виде силы Fк, приложенной к центру колеса и сообщающей поступательное движение колесу, а вместе с ним и всему поезду.
Сила тяги всего электровоза в первом приближении равна сумме сил тяги всех обмоторенных осей. однако следует учитывать, что при неустановившемся движении сила тяги выполняет работу не только на преодоление сил трения и сообщения ускорения поезду, но и на сообщение ускорения вращающимся частям поезда. Т.е. можно записать
Fу = Fк – åFин.вр.
Силы инерции вращающихся частей Fин.вр пропорциональны моменту инерции вращающихся частей и обратно пропорциональны радиусу инерции. Следовательно, справедливо выражение
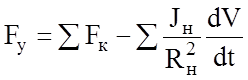 .
.
Здесь учтены только моменты инерции немоторных колесных пар, т.к. моменты инерции обмоторенных колесных пар и якорей ТД учтены в формуле для Мк.
Тяговая характеристика является нелинейной функцией скорости. Поэтому для оценки тяговых и тормозных свойств ЭПС существует понятие жесткости тяговой характеристики
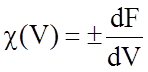 .
.
Знак "плюс" соответствует тяговому режиму, знак "минус" – электрическому торможению. Величина жесткости прежде всего зависит от системы возбуждения ТД.
Понятие "жесткость" позволяет определить изменение силы тяги со скоростью в виде приращения
dF = c(V)dV.
Это соотношение позволяет решать практические задачи по оценке тяговых и тормозных свойств ЭПС в различных условиях. Например, можно определить, насколько изменяются тяговые свойства локомотива вследствие разброса тяговых характеристик двигателей. Зная зависимости F(M), M(Ф), Ф(I), I(r) можно записать:
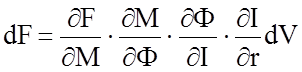 ,
,
т.е. жесткость тяговой характеристики равна произведению жесткостей всех ее составляющих. Нелинейность зависимости силы тяги от момента на валу ТД определяется нелинейной зависимостью потерь в тяговой передаче.
4.2. Реализация силы тяги с учетом упругой деформации колеса и рельса.
Вследствие деформации колеса и рельса при взаимодействии, колесо в действительности опирается на рельс некоторой поверхностью. Процесс деформации очень сложен, а теоретические выражения, описывающие процесс взаимодействия колеса и рельса получены только для простейших случаев сочетания профилей колеса и рельса. Основу решения проблемы положил физик Г. Герц в 1882 г.
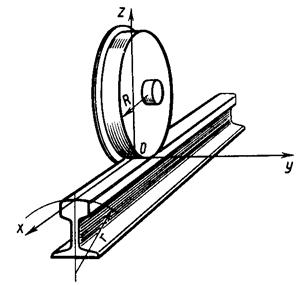 Рассмотрим идеализированный
случай упругого взаимодействия колеса и рельса, полагая их материал изотропным.
Начнем с неподвижного колеса. Расположим оси координат как показано на рисунке.
Т.к. стандартный ж.д. рельс имеет в поперечном сечении радиус головки
300 мм, представим колесо и рельс в виде двух бесконечных цилиндров,
расположенных во взаимно перпендикулярных плоскостях и имеющих, соответственно,
радиусы R и r.
Рассмотрим идеализированный
случай упругого взаимодействия колеса и рельса, полагая их материал изотропным.
Начнем с неподвижного колеса. Расположим оси координат как показано на рисунке.
Т.к. стандартный ж.д. рельс имеет в поперечном сечении радиус головки
300 мм, представим колесо и рельс в виде двух бесконечных цилиндров,
расположенных во взаимно перпендикулярных плоскостях и имеющих, соответственно,
радиусы R и r.
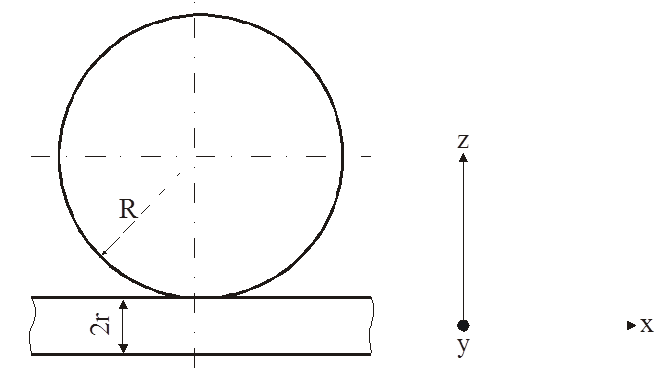 Рассмотрим проекцию
колеса на плоскость XOZ. Предположим, что под действием
силы Gк произошла деформация колеса
на величину z1. Длину проекции
поверхности взаимодействия колеса и рельса на плоскость XOZ
обозначим 2х. Рассмотрим треугольники АВО' и BОO'. Тре
Рассмотрим проекцию
колеса на плоскость XOZ. Предположим, что под действием
силы Gк произошла деформация колеса
на величину z1. Длину проекции
поверхности взаимодействия колеса и рельса на плоскость XOZ
обозначим 2х. Рассмотрим треугольники АВО' и BОO'. Тре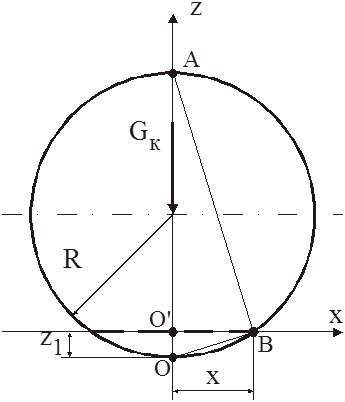 угольники подобны,
следовательно можно записать:
угольники подобны,
следовательно можно записать:
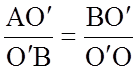 ;
;
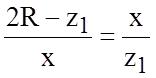 .
.
Так как z1 << R, то можно записать
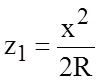
Рассматривая деформацию рельса в плоскости YOZ, по аналогии можно записать
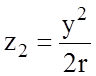 .
.
Суммарная деформация колеса и рельса
D = z1 + z2 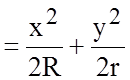 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.