Определение и содержание науки о тяге поездов. Уравнение движения поезда. Сопротивление движению поезда. Образование и реализация силы тяги. Торможение, страница 10

Обозначив относительную скорость упругого перемещения волокон бандажа 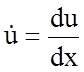; фактическую скорость перемещения волокон бандажа по опорной поверхности 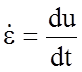 можно записать:

.

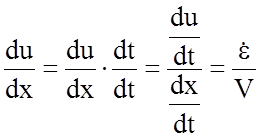4.4. Реализация силы тяги. Срыв сцепления.

Согласно исследованиям Ф.Картера касательная сила F_к, возникающая в режиме тяги, по опорной площадке при взаимодействии движущегося идеально упругого гладкого колеса с силой нажатия G_к на рельс, в первом приближении пропорциональна относительной скорости упругого смещения волокон материалов бандажа и рельса:

,

причем коэффициент пропорциональности k зависит от

–  силы нажатия колеса на рельс G_к;

–  диаметра колеса D_к;

–  упругих свойств материалов бандажа и рельса;

–  размеров и ориентации контактной площадки;

–  отношения текущего значения силы F_к к ее максимальному значению, определяемому коэффициентом трения покоя m₀ (F_сц max = m₀G_к).

Таким образом, сила F_к будет возрастать пропорционально относительной скорости смещения до достижения максимально возможного значения F_сц max. По мере приближения силы к этому значению зона сцепления на опорной площадке уменьшается; сил сцепления уже не хватает для сдерживания взаимного смещения волокон материала бандажа и рельса; зона упругого скольжения растет. Как только зона сцепления обратиться в точку, что соответствует значению  происходит срыв сцепления.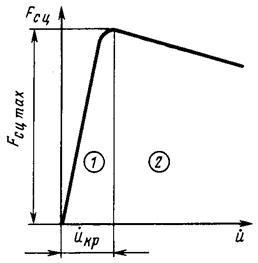

По Картеру  наступает при .

Таким образом, на рисунке можно выделить две области:

*  область 1, где  – происходит упругое смещение контактирующих материалов бандажа и рельса, что соответствует нормальной реализации силы тяги (область сцепления);

*  область 2, где  – происходит упругое скольжение контактирующих материалов бандажа и рельса, что соответствует срыву сцепления (область боксования).

4.5. Практическая оценка коэффициента сцепления.

Рассмотренные выше соотношения справедливы для идеализированных случаев профиля поверхности бандажа и рельса. В реальных условиях поверхность катания колеса имеет конусность переменной величины; поверхность катания рельса имеет наклон внутрь колеи. Кроме этого на коэффициент сцепления влияет множество случайных и неслучайных факторов. Среди них следует отметить следующие:

*  материал бандажа и рельса, их однородность;

*  состояние контактирующих поверхностей;

*  износ контактирующих поверхностей;

*  скорость движения;

*  соединение ТД;

*  вид тягового привода;

*  режим работы ТД.

Все это делает практически невозможным вывод аналитического выражения для расчета коэффициента сцепления.

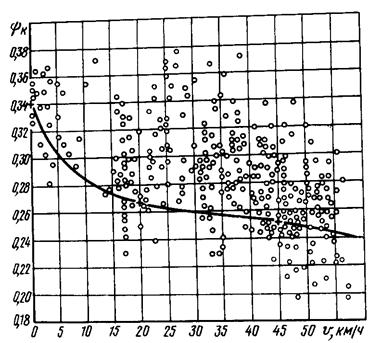
Для практических целей используются выражения зависимости коэффициента сцепления от скорости движения полученные эмпирическим, т.е. опытным путем. Для определения зависимости коэффициента сцепления от скорости движения на полигоне проводят ряд тяговых испытаний ЭПС, в ходе которых добиваются срыва сцепления при различных погодных условиях, различных скоростях движения и различных износах бандажа. При этом фиксируется сила тяги, при которой произошел срыв сцепления. На поле зависимости коэффициента сцепления от скорости движения получаем множество точек.

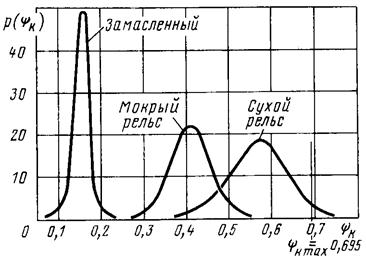
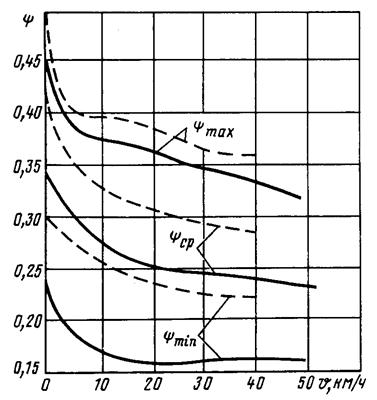
По мере накопления данных производят их обработку методами математической статистики, в результате получают кривые вероятности распределения коэффициента сцепления при различных скоростях движения и различных условиях сцепления. Обработав все результаты, получают кривые зависимости коэффициента сцепления от скорости движения. После математической обработки полученных кривых выводится выражения, наиболее близко их описывающие.

В Правилах тяговых расчетов МПС рекомендует для решения практических задач использовать для вычисления коэффициента сцепления выражения вида

,

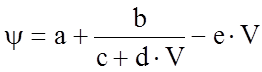где коэффициенты a, b, c, d ,e определяются типом ЭПС.

Приведенное выражение получено давно, когда еще не произошло широкого распространения ПЭВМ, которые обладают значительным быстродействием и удобством использования. Хотя, как известно из математики любую гладкую кривую (без экстремумов) можно представить как полином степени n:

.

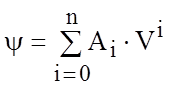Степень полинома зависит от вида кривой и точности, требуемой для практических расчетов. Коэффициенты полинома А_i нетрудно рассчитать с помощью многочисленных математических пакетов для ЭВМ.

4.6. Факторы, влияющие на реализацию силы тяги.

Реализация силы тяги определяется коэффициентом сцепления, реализуемым электровозом в целом. Ранее были рассмотрены факторы, влияющие на величину коэффициента сцепления одного колеса. С учетом того, что не только все колесные пары электровоза, но и даже отдельные колеса одной и той же колесной пары находятся в неодинаковых условиях, силу сцепления, реализуемую электровозом в целом нельзя найти простым перемножением величины силы сцепления одного колеса на количество колес электровоза. Она будет всегда меньше указанного произведения:

F_сц э < N_к × F_к, но ,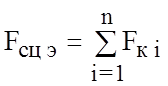

т.е. силу сцепления электровоза в целом следует определять как алгебраическую сумму сил, реализуемых отдельными колесами.

Поскольку реализация сил сцепления определяется прежде всего реализацией коэффициента сцепления, то можно, по аналогии с факторами, влияющими на коэффициент сцепления, выделить три основных группы параметров, влияющих на реализацию силы сцепления:

*  изменение силы давления колеса на рельс;

*  геометрические характеристики взаимодействующих поверхностей колеса и рельса;

*  состояние взаимодействующих поверхностей колеса и рельса.

В свою очередь, каждая группа факторов подразделяется на подгруппы и отдельные факторы.

Изменение силы давления колеса на рельс:

*  статическая неравномерность распределения массы электровоза по отдельным колесным парам и отдельным колесам – вызвана неизбежными неточностями при монтаже оборудования внутри кузова электровоза, а так же отклонениями при изготовлении отдельных деталей;

*  вертикальные колебания электровоза, вызванные прохождением неровностей пути – зависят от геометрической и динамической характеристики пути, скорости движения и состояния рессорного подвешивания электровоза, включая гасители колебаний;