Сущность этого коэффициента можно понять при рассмотрении энергетики движения экипажа. Кинетическая энергия движущегося экипажа складывается из кинетической энергии поступательного движения, которая пропорциональна квадрату линейной скорости, и кинетической энергии вращательного движения, которая пропорциональна квадрату угловой скорости:
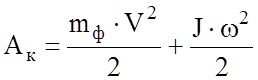 ,
,
где mф – фактическая масса экипажа (масса в состоянии покоя);
J – момент инерции вращающейся массы.
Предположим, что у нашего экипажа обмоторенной является только одна ось. В этом случае кинетическая энергия вращающихся частей складывается из кинетической энергии якоря тягового двигателя, кинетической энергии обмоторенной оси (имеются вращающиеся шестерни редуктора) и кинетической энергии необмоторенной колесной пары:
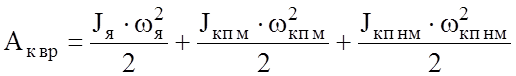 .
.
Для многоосного локомотива, как и для поезда в целом необходимо просуммировать составляющие кинетической энергии:
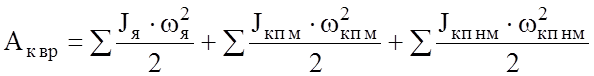 .
.
Угловая скорость вращения пропорциональна линейной скорости движения центра, относительно которого происходит вращение:
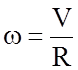 ,
,
где R – радиус вращения рассматриваемой точки.
Для приведения частоты вращения якоря тягового двигателя к частоте вращения колесной пары, которую он приводит во вращение, в формулу вводится поправочный коэффициент, равный передаточному числу редуктора:
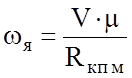 .
.
Таким образом, формула для полной кинетической энергии приобретет вид:
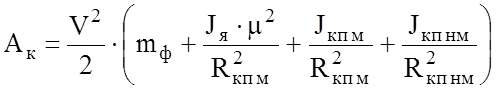 .
.
Из формулы
следует, что величина ![]() имеет размерность массы.
Поэтому можно записать
имеет размерность массы.
Поэтому можно записать
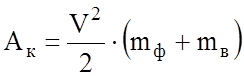 ,
,
где mв – эквивалентная масса вращающихся частей.
Таким образом, принимая отношение
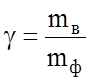
за коэффициент инерции вращающихся частей имеем
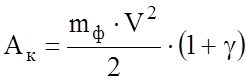 .
.
То есть коэффициент инерции вращающихся частей показывает, насколько увеличивается кинетическая энергия экипажа (поезда) за счет наличия в нем вращающихся частей. Следует отметить, что полученное определение справедливо только для тех вращающихся частей, вращение которых зависит от поступательного движения поезда. Так, коэффициент инерции электровоза не учитывает инерционность вентиляторов принудительного охлаждения тяговых двигателей, а также инерционность других вспомогательных машин.
В литературе можно встретить термин эквивалентная масса mэ – это фиктивная масса, которой должно обладать тело без вращающихся частей, но обладающее такой же кинетической энергией, что и тело массой mф, но имеющее вращающиеся части:
mэ = mф × (1+g).
Кинетическая энергия экипажа в процессе движения под воздействием суммы сил åF будет изменяться. Это изменение равно работе, совершаемой равнодействующей сил на каком либо отрезке пути. Предположим, что экипаж переместился на расстояние ds, тогда
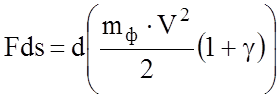 .
.
Продифференцировав правую часть выражения и разделив обе части на ds получим:
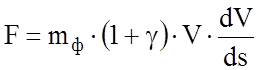 .
.
Учитывая, что
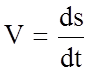 ,
,
можно записать
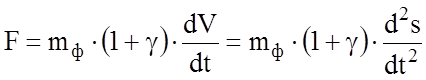 .
.
Эти два выражения позволяют интегрировать уравнение движения по пути и времени и являются двумя формами уравнения движения поезда.
На практике, для удобства, (во избежание громоздких вычислений) используют уравнение движения поезда в удельных величинах. Для получения такой разновидности уравнения разделим правую и левую части на массу:
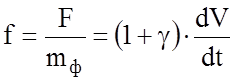 .
.
Здесь f – удельная равнодействующая сил, то есть сила, приходящаяся на 1 т массы поезда.
Помимо физической системы единиц, существует еще и техническая (железнодорожная), которая сложилась исторически по мере развития науки о тяге поездов. В этой системе вместо массы фигурирует вес. Учитывая, что Q = m×g, можно записать
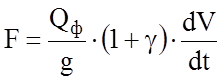 ;
;
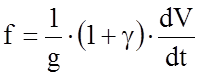 .
.
Обозначив
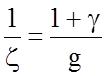 ,
,
получим
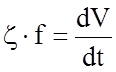 .
.
Здесь z – коэффициент, соответствующий ускорению единицы веса поезда при действии на него одной тонно-силы. Обозначается греческой буквой "дзета".
2.2. Уравнение движения поезда.
Перейдем к реальному поезду, состоящему из локомотива и вагонов, соединенных между собой и с локомотивом посредством автосцепок, которые представляют собой упруго-жесткие связи. Реальный поезд в продольном направлении имеет число степеней свободы, равное числу вагонов в поезде из-за различия характеристик поглощающих аппаратов и различного износа деталей автосцепных приборов. Следовательно, вагоны могут перемещаться друг относительно друга и относительно центра тяжести поезда.
Рассмотрим поступательное движение поезда под воздействием внешних сил:
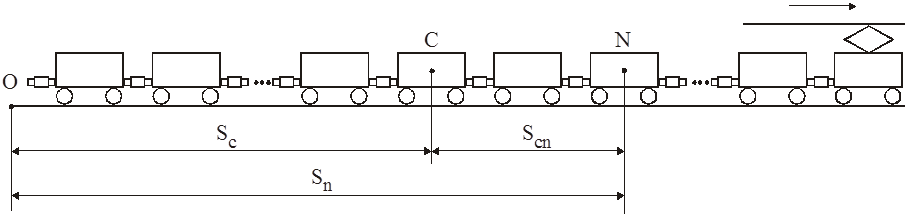
sc – координата центра тяжести поезда относительно начала координат;
sn – координата центра тяжести n-го вагона относительно начала координат;
scn – координата центра тяжести n-го вагона относительно центра тяжести поезда.
sc характеризует полезное перемещение поезда, scn – относительное перемещение вагонов, на которое дополнительно расходуется энергия.
Координату центра тяжести любого вагона можно определить как сумму координаты центра тяжести поезда относительно начала отсчета и координаты центра тяжести этого вагона относительно центра тяжести поезда. Поезд в целом характеризуется системой уравнений:
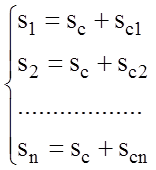 .
.
Ускорение n-го вагона складывается из ускорения центра тяжести поезда и ускорения n-го вагона относительно центра тяжести поезда. Для нахождения ускорения n-го вагона дважды продифференцируем выражение по времени:
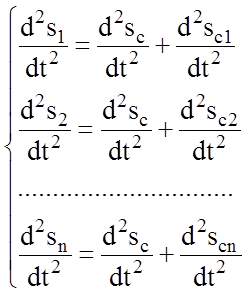 .
.
Подставляя полученное выражение для ускорения в уравнение движения поезда, получим:
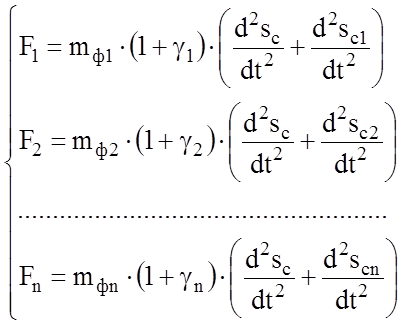 .
.
Таким образом, движение поезда характеризуется системой из n уравнений. В практических расчетах практически никогда не используют приведенное выше выражение, т.к. получить выражение для относительных перемещений вагонов крайне сложно. Для этого необходимо использовать аппарат теории вероятностей и математической статистики.
2.3. Методы интегрирования уравнения движения поезда.
Все практические вопросы тяги поездов: определение массы состава, скоростей движения, времени прохождения отдельных перегонов, решение тормозных задач, определение расхода электроэнергии и топлива решаются при помощи уравнения движения поезда.
В 1898 г. появились графические способы интегрирования уравнения движения поезда. В России был опубликован способ Шведе, а во Франции способ Дедуи, однако оба эти способа не получили широкого практического применения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.