Определение и содержание науки о тяге поездов. Уравнение движения поезда. Сопротивление движению поезда. Образование и реализация силы тяги. Торможение, страница 19

Все перечисленные методы имеют достоинства и недостатки и выбор метода зависит от поставленной задачи. Графоаналитический метод практически отмирает, так как предполагает использование тягового расчета и "ручного" подсчета расхода электроэнергии по кривым движения поезда. Гораздо проще сделать это на ЭВМ при выполнении тягового расчета.

6.2. Аналитический метод определения расхода электроэнергии.

При движении по перегону ТД ЭПС производят преобразование электрической энергии в механическую, которая затрачивается на преодоление сил сопротивления движению и сообщение поезду кинетической энергии. В процессе преобразования неизбежны потери энергии. Можно выделить следующие составляющие расхода электроэнергии при движении поезда по перегону:

  преодоление сил сопротивления движению основного и дополнительного (А_w);

  собственные нужды (А_сн);

  потери при пуске (А_п);

  потери в ТД и преобразовательных установках (если таковые имеются) (А_тд);

  потери в тормозах (А_т):

А = А_w + А_сн + А_п + А_тд + А_т.

Если ЭПС оборудован системой рекуперативного торможения, то потери энергии в тормозах будут уменьшены на величину энергии, возвращенной в контактную сеть. Уравнение в этом случае примет вид:

А = А_w + А_сн + А_п + А_тд + А_т – А_р.

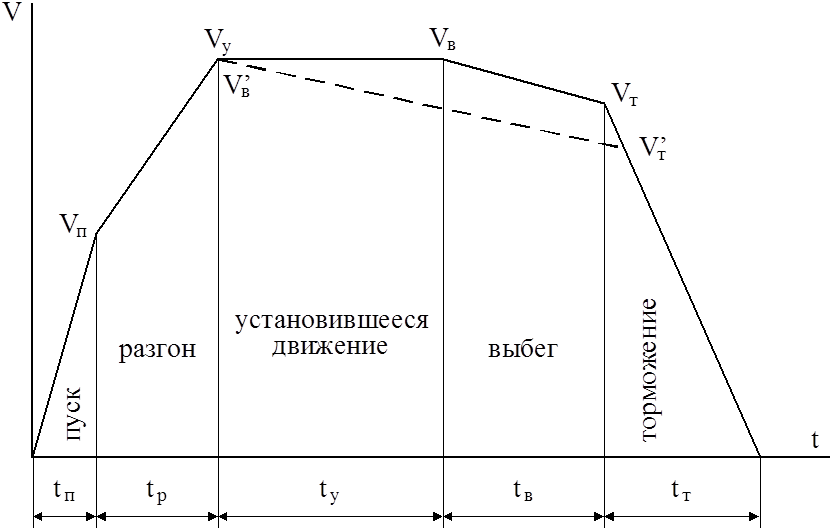
При движении поезда по перегону можно выделить следующие режимы:

  пуск;

  разгон;

  установившееся движение;

  выбег;

  торможение.

Под термином "пуск" следует понимать:

  для ЭПС постоянного тока, имеющего реостатное регулирование напряжения (ступенчатое или плавное) – разгон до выхода ТЭД на безреостатную характеристику;

  для ЭПС переменного тока с коллекторными ТЭД и ступенчатым регулированием напряжения – разгон до позиции, на которой допускается длительная работа;

  для ЭПС переменного тока с коллекторными ТЭД и с зонно-фазовым регулированием напряжения – разгон до минимального угла регулирования любой зоны, на которой регулирование прекращается;

  для ЭПС с асинхронными ТЭД – разгон до выхода на режим реализации постоянства мощности ТЭД.

На различных перегонах могут отсутствовать режимы разгона, установившегося движения и выбега. Рассмотрим с энергетической точки зрения режимы движения поезда по перегону.

При пуске и разгоне из КС потребляется энергия, которая расходуется на преодоление сопротивления движению и увеличения кинетической энергии поезда:

.

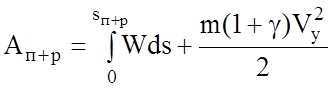При установившемся движении под током энергия расходуется только на преодоление сопротивления движению, поэтому, с учетом того, что V_у = V_в, формула приобретет вид

.

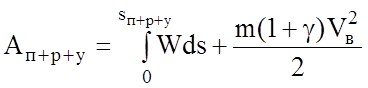После отключения ТД запасенная кинетическая энергия расходуется на преодоление сил сопротивления движению. При этом скорость снижается до V_т. Уравнение энергетического баланса имеет вид:

.

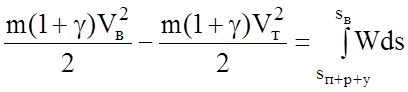С учетом того, что на участке выбега на преодоление сил сопротивления движению расходуется запасенная ранее кинетическая энергия, можно записать:

.

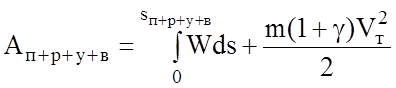Для остановки поезда необходимо, чтобы его кинетическая энергия стала равной нулю. Следовательно, на участке торможения остаток кинетической энергии должен быть преобразован в другой вид энергии. При этом часть энергии затрачивается на преодоление сил сопротивления движению. Таким образом, полученное выше выражение является выражением для расхода энергии для движения поезда по перегону без учета потерь.

Для учета энергии рекуперации предположим, что процесс рекуперации возможен до скорости, равной нулю. Тогда:

.

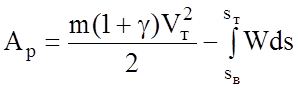Сравнивая полученные выражения можно сделать вывод о том, что для "идеального" ЭПС, оборудованного системой рекуперативного торможения затраты энергии на движение по перегону будут равны затратам на преодоление сил сопротивления движению на всем перегоне:

.

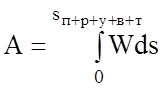Для реального ЭПС при движении в режиме тяги и рекуперативного торможения неизбежны потери в ТД и тяговой передаче. Поэтому в формулы необходимо ввести соответствующие коэффициенты:

;

.

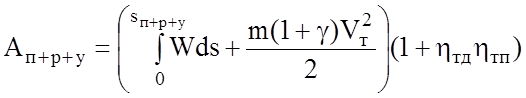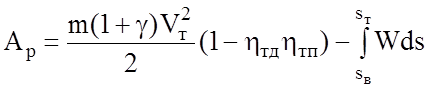В том случае, если ЭПС имеет тяговый привод, который предусматривает питание тяговых двигателей через преобразователь во всем диапазоне скоростей (например, ЭПС переменного тока с коллекторными ТЭД; ЭПС с асинхронными ТЭД), то необходимо учитывать и его КПД:

;

.

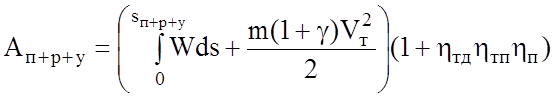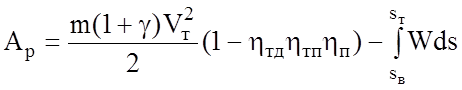В режиме пуска часть энергии теряется в преобразователе или пусковых резисторах. Учет потерь в преобразователе производится с помощью его КПД, в реостатах – коэффициента пусковых потерь:

;

.

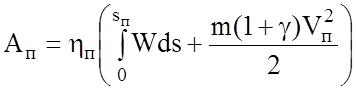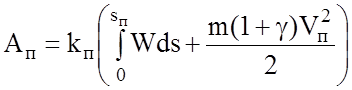Расход энергии на собственные нужды зависит от мощности потребителей и времени нахождения поезда на перегоне:

.

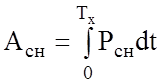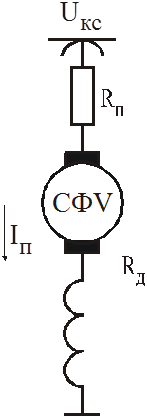Следует отметить, что величины КПД преобразователя, ТЭД, тяговой передачи, используемые в формулах не являются постоянными величинами. Для повышения достоверности вычислений следует рассматривать КПД как функцию мощности, реализуемой ТЭД или передаваемой преобразователем или тяговой передачей.

Для получения представления о коэффициенте пусковых потерь изобразим графически уравнение, описывающее пуск ТД при неизменном пусковом токе, в функции времени без учета магнитных и механических потерь. Для этого запишем уравнение электрического равновесия для режима пуска:

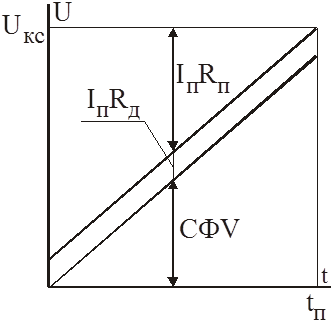
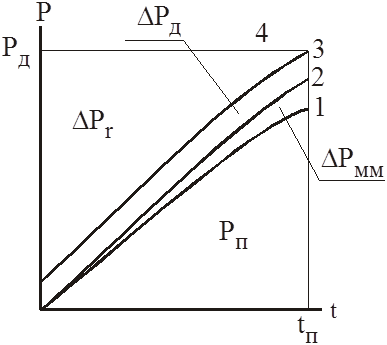
U_кс = CФV + I_пR_д + I_пR_п.

Так как ток постоянен, следовательно, постоянен и магнитный поток. Линия, характеризующая величину СФV является прямой, проходящей через начало координат. Несколько выше и параллельно ей будет расположена линия, характеризующая падение напряжения на активных сопротивлениях обмоток ТД. Как следует из уравнения, величина падения напряжения на пусковом резисторе будет убывать с ростом скорости. Эта величина равна разности ординат горизонтальной линии, характеризующей напряжение, приложенное к ТД и линии I_пR_д. В точке пересечения линий U_д и I_пR_д процесс пуска закончится. Далее к ТД приложено полное напряжение.

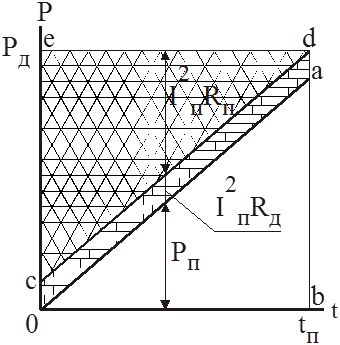Домножим величины, откладываемые по оси ординат на ток ТД. При этом мы получим диаграмму изменения мощностей. Из которой следует, что при увеличении скорости мощность потерь на активных сопротивлениях обмоток ТД постоянна, а мощность потерь в пусковых сопротивлениях уменьшается. Так как энергия равна интегралу от мощности по времени, то площади, ограниченные соответствующими линиями характеризуют затраты энергии на нагревание воздуха (четырехугольник а0еd) и полезную работу (треугольник а0b).