При моделировании пуска или электрического торможения электропоездов с контакторно-реостатной системой регулирования удобно интегрирование уравнения движения по току тягового двигателя (косвенное интегрирование по скорости). При этом
,
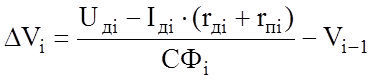где Uдi – напряжение, прикладываемое к тяговому двигателю на i-м шаге;
Iдi × (rдi + rпi) – падение напряжения на активном сопротивлении обмоток тягового двигателя и пускового резистора;
Сфi – магнитный поток, соответствующий току Iдi.
Использование тока тягового двигателя в качестве независимой переменной при интегрировании уравнения движения поезда имеет еще одно преимущество перед остальными способами – возможность уменьшения памяти ЭВМ, необходимой для хранения тяговых и тормозных характеристик ЭПС и уменьшения предварительной работы по обработке характеристик и вводу их в ЭВМ.
Поскольку решение уравнения движения поезда, как правило, подразумевает выбор оптимального с точки зрения расхода электроэнергии режима движения поезда, то необходимо иметь два семейства характеристик – тяговые (тормозные) и токовые. Как известно, сила тяги на ободе колеса определяется выражением
Fк = СФк × Iд,
скорость движения
.
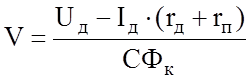В оба выражения входит величина нагрузочной характеристики тягового электродвигателя СФк, приведенная к ободу колеса. Следовательно, оба семейства характеристик можно описать имея зависимость СФк = ¦(Iв). В этом случае объем требуемой памяти ЭВМ и объем предварительных вычислений уменьшается как минимум вдвое. Для вычислений на ЭВМ зависимость СФк = ¦(Iв) целесообразно представить в виде степенного полинома вида
.
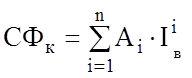Коэффициенты полинома Аi нетрудно получить с использованием одного из математических компьютерных пакетов. Степень полинома n выбирается исходя из требуемой точности вычислений.
Таким образом, в режимах тяги и электрического торможения уравнение движения поезда для практических задач целесообразно интегрировать по току тягового электродвигателя; в режимах тяги и механического торможения – по скорости. При подходе к установившемуся режиму шаг интегрирования следует уменьшать. Критерием выбора величины шага интегрирования может быть точность расчетов, например допустимая погрешность прицельного торможения у остановочного пункта или длина элемента профиля. В установившихся режимах интегрировать уравнение движения следует по времени или пути.
Численные методы. Сущность их заключается в замене нелинейного дифференциального уравнения движения поезда линейным дифференциальным, решение которого с достаточной для практики точностью приближается к решению нелинейного уравнения, то есть в линеаризации уравнения движения поезда. Основным допущением, позволяющим производить линеаризацию, является принцип малых отклонений входящих в уравнение координат от тех значений, которые приняты в качестве исходных для линеаризации.
Известно много различных методов численного интегрирования дифференциальных уравнений: Чаплыгина, Адамса, Рунге-Кутта, Милна и других. Эти методы обеспечивают сравнительно высокую степень точности, но требуют большого объема подготовительных работ. В тяговых расчетах используют менее точные, но более простые – метод Эйлера и разложения функции v(s) в ряд Тейлора. Зависимости fк = f(V) и b = f(V) для этих методов описываются полиномами.
Для любого метода численного интегрирования расчет конечно-малых приращений времени производится по формуле:
.
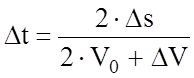Метод Эйлера. Запишем уравнение движения поезда в виде:
,
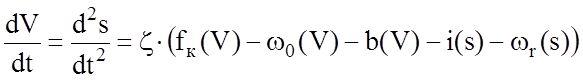где wr(s) – зависимость сопротивления движению от кривых в функции пути.
Преобразуем уравнение:
.
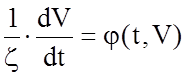Интервал времени, на котором решается уравнение разделим на n равных частей:
.
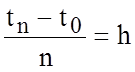Производную в каждой точке кривой v(t) заменяем конечным приращением. С учетом того, что правую часть уравнения на каждом шаге считаем постоянной для n-го шага имеем:
,
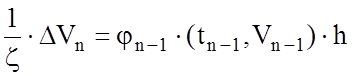то есть искомая функция на каждом шаге заменяется касательной линией, проведенной к точке, соответствующей началу шага.
Скорость движения и координата на n-м шаге:
Vn = Vn-1 + h × z × (fк – wо – b – i – wr);
sn = sn-1 + Vn-1 × Dt.
Таким образом, сущность метода Эйлера сводится к аппроксимации интегральной кривой v(t) последовательно сопряженными касательными.
Метод Эйлера применяется в системах автоведения поезда.
Решение уравнения движения поезда разложением в ряд Тейлора. Как известно, функцию вида y = j(x) можно разложить в ряд Тейлора:
,
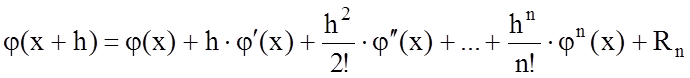где Rn – остаточный член ряда;
n – приращение независимой переменной.
Применительно к уравнению движения поезда выражение примет вид:
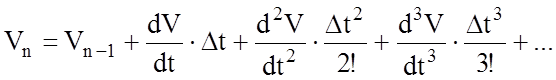
По методике ПТР разложение в ряд Тейлора производится до третьего члена включительно, а в качестве независимой переменной интегрирования уравнения движения принимается V при малых скоростях и s при высоких. Такое разграничение объясняется тем, что при увеличении скорости движения равнодействующая сил fy ® 0, а следовательно Dt ® ¥. При независимой переменной V разложение функции V(s) в ряд Тейлора приобретает вид:
.
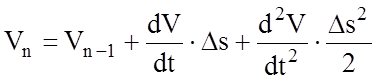В полученном
уравнении остались дифференциалы, от которых мы так старательно стремились
избавиться. В данном случае величина 
является
коэффициентом наклона кривой скорости к оси времени, а величина 
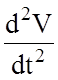– соответственно, коэффициентом
наклона кривой ускорения.
Приращение пути на любом шаге
.
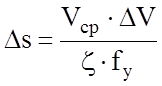Так как при расчетах ограничиваются тремя членами ряда, то выражения для вычисления скорости движения и пути обеспечивают достаточную точность при соблюдении следующих условий:
1. При разгоне до выхода на автоматическую характеристику интегрирование ведется по скорости. При этом допустимое приращение скорости DVдоп = 3¸5 км/ч.
2. При более высоких скоростях интегрирование ведется по пути. При этом за шаг интегрирования принимается весь элемент профиля, если
<
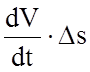3¸5 км/ч; 
<
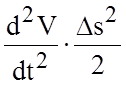0,1¸0,5 км/ч.
При невыполнении условия шаг интегрирования следует уменьшить.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.