Определение и содержание науки о тяге поездов. Уравнение движения поезда. Сопротивление движению поезда. Образование и реализация силы тяги. Торможение, страница 5

Решение уравнения движения поезда разложением функции в ряд Тейлора успешно применяется при тяговых расчетах для разработки графика движения поездов.

3. Сопротивление движению поезда.

На движущийся поезд действует многообразие сил, которые препятствуют его движению. Все эти силы имеют различную природу возникновения и характер действия. Одни силы неизменны во времени, другие изменяются (медленно или быстро). Многие из сил взаимосвязаны, другие случайны. В Теории электрической тяги принято оценивать суммарный эффект от сил, противодействующих движению поезда как сопротивление движению поезда. В соответствии с этим, сопротивлением движению поезда называют эквивалентную силу, приложенную к ободу колеса, на преодоление действия которой затрачивается такая же работа, как и на преодоление всех действительных сил, противодействующих движению поезда.

Сопротивление движению поезда принято разделять на основное и дополнительное, хотя следовало бы выделить еще добавочное сопротивление движению как разновидность дополнительного.

3.1. Основное сопротивление движению.

Основное сопротивление движению представляет собой сопротивление движению подвижного состава данного типа на прямолинейном горизонтальном открытом участке пути при любой скорости. Оно обусловлено трением в узлах подвижного состава, сопротивлением при взаимодействии подвижного состава и пути, а так же сопротивлением воздушной среды при отсутствии ветра.

Как известно, уравнение движения поезда можно интегрировать по времени, пути или скорости.

;

.

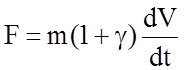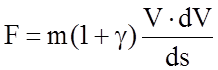Поэтому желательно иметь зависимость основного сопротивления движению поезда от этих величин. Скорость движения однотипных поездов на одном и том же участке может изменяться случайным, поэтому наиболее целесообразно иметь зависимость основного сопротивления движению поезда от скорости.

Установить зависимость основного сопротивления движению поезда от скорости, так же, как и зависимость коэффициента сцепления колеса с рельсом, практически очень сложно, так как слишком большое количество факторов определяет сопротивление движению. Поэтому в Теории электрической тяги пользуются эмпирическими формулами, которые дают лишь математическое ожидание основного сопротивления движению.

Основное удельное сопротивление движению, как, впрочем и полное рассчитывают отдельно для электровоза и состава:

W_o = W' + W".

Для практических расчетов, как уже говорилось ранее, используют удельное значение основного сопротивления движению поезда:

,

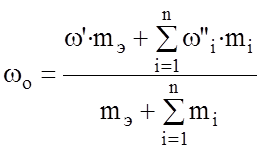где m_э и m_i – соответственно вес электровоза и вагона i-го типа.

В общем виде выражение для основного удельного сопротивления движению выглядит следующим образом:

.

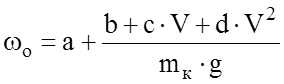Коэффициенты a, b, c, d зависят от типа подвижного состава и определяются опытным путем на основании статистической обработки кривых выбега. Из формулы следует, что кривая w_o = ¦(V) не проходит через ноль и имеет квадратическую составляющую зависимость от скорости (влияние аэродинамического сопротивления).

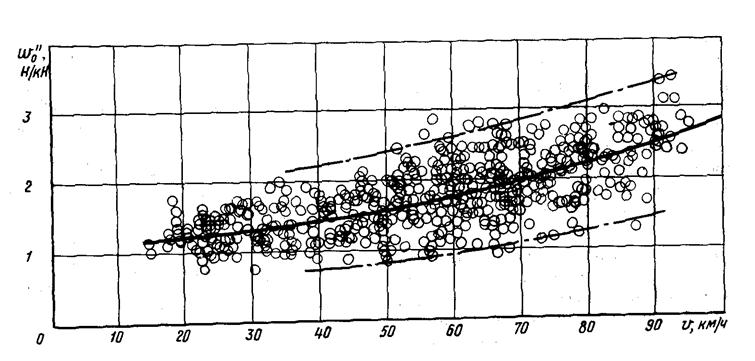
Как видно из рисунка опытные значения основного удельного сопротивления имеют значительный разброс от наиболее вероятного значения (эксперименты показали, что разброс достигает 50%). Однако формулы приведенные в ПТР для практических задач применимы.

Основное сопротивление движению поезда можно представить как сумму нескольких компонент:

-  сопротивление от трения в подшипниках (W_п);

-  сопротивление от трения качения колес по рельсам (W_к);

-  сопротивление от проскальзывания колес вследствие разности диаметров поверхностей катания, находящихся в данный момент в "работе" (конусность колес) (W_ск);

-  сопротивление от деформации пути и ударов колес на стыках и неровностях пути (например, при прохождении стрелочных переводов) (W_д);

-  сопротивление от воздушной среды (W_в);

-  сопротивление от колебаний подвижного состава (W_дин).

W_o = W_п + W_к + W_ск + W_д + W_в + W_дин.

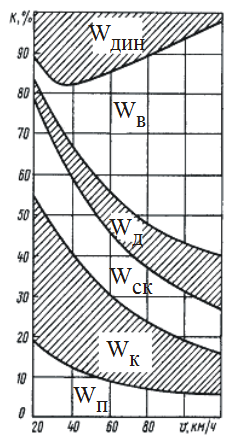На рисунке приведено распределение составляющих основного сопротивления движению для четырехосных вагонов.

Из рисунка следует, что основной составляющей сопротивления движению является сопротивление от воздушной среды.

Рассмотрим более подробно наиболее значимые составляющие основного сопротивления движению. Трение в подшипниках зависит от момента сил трения. Наиболее простой вариант, дающий представление о природе возникновения сопротивления движению от трения в подшипниках дает рассмотрение подшипника скольжения, который на данный момент сохранился только на грузовых электровозах (МОП). Сила трения пропорциональна коэффициенту трения и силе давления на ось колесной пары. Момент силы трения – плечу ее приложения. Поскольку сила W_п является порождением силы трения в подшипнике, следовательно можно приравнять их моменты:

,

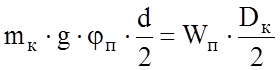следовательно

.

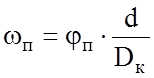Коэффициент трения зависит от скорости движения и вязкости смазки (верхняя линия – более вязкая смазка). Из рисунка видно, что подшипники скольжения имеют огромное сопротивление при трогании с места. Процесс образования трения в роликовых подшипников скорее напоминает образование трения качения колеса по рельсу, но несомненно, что со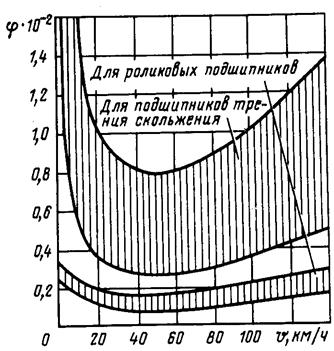противление в роликовых подшипниках значительно ниже, чем в подшипниках скольжения.

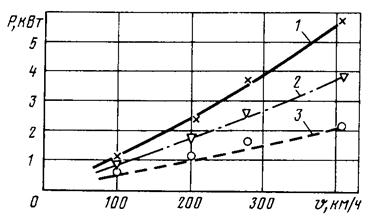При проектировании и обкатке скоростного поезда TGV были проведены опыты, из которых следует, что коэффициент трения зависит не только от скорости движения, но и пробега подшипника (1 – новый подшипник; 3 – пробег 250 тыс.км). Это объясняется тем, что в подшипнике происходит приработка взаимодействующих поверхностей.

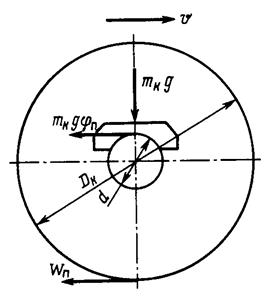
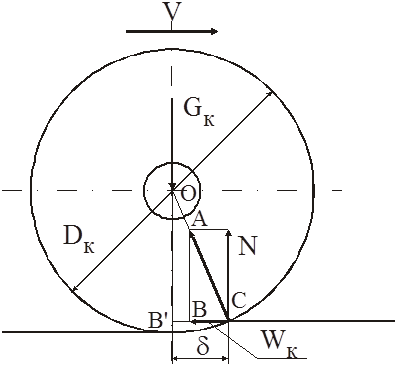Возникновение трения при качении колеса по рельсу обусловлено деформацией поверхностей катания, на что необходимо затрачивать энергию. Деформация поверхностей катания приводит к смещению точки приложения равнодействующей сил со стороны рельса на некоторую величину d по направлению движения колесной пары. Разложим равнодействующую сил сопротивления на две составляющие: направленную вертикально (она равна силе давления колеса на рельс) и направленную вдоль рельса (она то и является силой трения качения). Рассмотрим треугольники ОСВ' и АВС.