Значительно большее применение получил графический способ, предложенный группой русских инженеров, работавших в конторе опытов при Министерстве путей сообщения (способ МПС).
Графоаналитические способы расчёта скорости и времени хода поезда были предложены Васютынским (1903 г.), Чечоттом (1910 г.). Способ интегрирования уравнения движения поезда с разложением в ряды был предложен Н.Н. Дегтеревым (1919 г.), разработавшим в дальнейшем и несколько графических способов.
Кратко рассмотрим некоторые способы решения уравнения движения поезда, используемые на практике до сих пор.
Графический метод. Исторически первым методом, примененным для практических задач, был графический метод, предложенный группой русских инженеров, работавших в конторе опытов при Министерстве путей сообщения (способ МПС). Графический метод основан на принципе конечных приращений и геометрической связи диаграммы равнодействующих сил fy(V) и интегральной кривой V(s), существующей благодаря общей зависимости сил fy и пути s от скорости.
Графический метод дает сравнительно невысокую точность расчетов и требует больших затрат времени. В настоящее время этот метод утрачивает свое значение и заменяется численными расчетами на ЭВМ.
Аналитический метод. Поскольку уравнение движения поезда существует в аналитическом виде, то логично решать его аналитическим методом. Запишем уравнение движения поезда, развернув его правую часть:
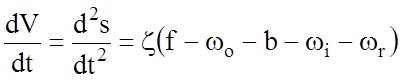 ,
,
где f и b – соответственно удельная сила тяги и торможения;
wо, wi, wr – сопротивление движению, соответственно основное, от уклонов, кривых.
Из анализа приведенного выражения следует, что уравнение движения поезда возможно интегрировать по:
- пути;
- скорости;
- времени.
Для реализации этих возможностей необходимо иметь аналитические зависимости всех входящих в него составляющих, причем, зависимости необходимо иметь от той переменной, по которой производится интегрирование.
Из всех составляющих уравнения движения только для основного сопротивления движения существуют аналитические зависимости в функции скорости (wо = f(V)). Для механического колодочного торможения существуют аналитические зависимости коэффициента трения от скорости движения, поэтому получить зависимость b = f(V) так же нетрудно.
Тяговые, а так же тормозные характеристики электрического торможения большинства типов ЭПС, как правило, представлены в графическом или табличном виде в функции скорости. Для использования этих характеристик при аналитическом методе решения уравнения движения необходимо преобразовать их в аналитические выражения, что нетрудно сделать с использованием современных математических компьютерных пакетов.
Зависимость сопротивления движению от уклонов обычно представлена в функции пути. Зависимость сопротивления движению от кривых может быть представлена одновременно в функции пути и скорости:
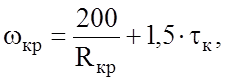
где Rкр – радиус кривой;
tк – непогашенное ускорение в кривой.
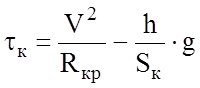 ,
,
где h – возвышение наружного рельса в кривой;
Sк – расстояние между кругами катания колес;
g – ускорение свободного падения.
Наиболее простая и наглядная формула получается при отсутствии возвышения наружного рельса:
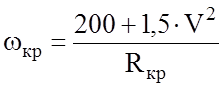 .
.
Получить зависимости сопротивления движению от уклонов и кривых в функции скорости возможно только в том случае, если уже имеется зависимость скорости от пути.
Из сказанного выше следует сделать вывод, что наиболее просто уравнение движения поезда может быть решено аналитическим методом с использованием в качестве независимой переменной скорости движения.
На практике решение уравнения движения поезда аналитическим методом в чистом виде практически не встречается. Для практических задач используются менее точные методы, сущность которых сводится к замене дифференциалов конечными приращениями. Уравнение движения в этом случае приобретает вид:
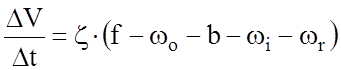 .
.
Величины, входящие в правую часть уравнения на каждом шаге расчета принимаются постоянными – т.е. производится кусочно-линейная аппроксимация интегральных кривых. Проанализируем, какую из переменных наиболее рационально принимать за независимую.
В случае использования в качестве независимой переменной скорости расчет на каждом шаге производится в следующем порядке: DVi ® Dti ® Dsi.
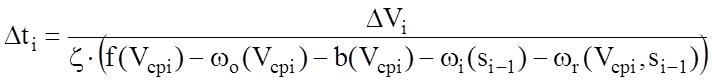 ;
;
Dsi = Vсрi × Dti.
Здесь Vсрi – средняя скорость движения на i-м шаге расчета:
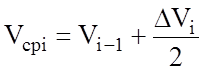 .
.
Из выражения для приращения времени видно, что величина сопротивления движению от уклонов и кривых "запаздывают" на один шаг расчета, что приводит к некоторой погрешности вычислений. Кроме этого, данный метод неприменим при установившемся режиме движения (fу ® 0 Þ Dt ® ¥).
В случае использования в качестве независимой переменной времени расчет на каждом шаге производится в следующем порядке: Dti ® DVi ® Dsi.
DVi = Dti × z × (f(Vi-1) – wo(Vi-1) – b(Vi-1) – wi(si-1) – wr(Vi-1,si-1);
Dsi = Vсрi × Dti.
В данном случае "запаздывают" все составляющие удельной ускоряющей силы, но нет проблем с установившимся режимом движения.
В случае использования в качестве независимой переменной пути расчет на каждом шаге производится в следующем порядке: Dsi ® Dti ® DVi.
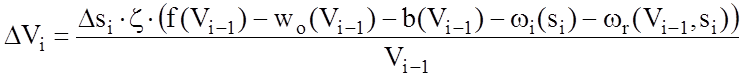 ;
;
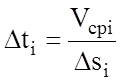 .
.
Как следует из приведенных выше выражений, наименьшую погрешность должно дать интегрирование уравнения движения по скорости. Однако этот способ не позволяет интегрировать уравнение при установившемся режиме движения. Для исключения значительных погрешностей вычислений при подходе к установившемуся режиму движения (вследствие больших приращений пройденного пути возможен "пропуск" элементов профиля) следует во-первых, уменьшать шаг интегрирования, и, во-вторых – что при попадании величины удельной ускоряющей силы в некоторый диапазон fу min < fу < fу max следует считать режим движения установившимся. Величина диапазона выбирается исходя из требуемой точности расчетов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.