Характеристика объемных приводов. Обеспечение синхронности и последовательности движения гидропневмодвигателя. Теория рабочих процессов в гидроприводах, страница 16

Рассмотрим частный случай, когда инерционная сила действующая… по сравнению с движущими силами и силами позиционной нагрузки. Силой гидравлического сопротивление и переменная составляющая сил трения

Где Спр это приведенная жесткость позиционной нагрузки. Из уравнения 8 получаем У=А поршня на Спр ну и на уигрек по дэ тэ. Полученнные значения можно подставит..

Динамика пневматическихй протончно

Обычно принимают 3. Первое из ни х  … сил инерции обусловлено и мгновенное значение скортси раоокоторый

Рассматриваются как квизу ст

Второе д вв происходит по изо

На

Средним между изотермическими и

Рассмотрим динамику. Составление уравнений описывающих динамику проводим по:

1)

2)

В случае переменного объема переменной камеры необходимо

Уравнение движения жидкости в трубопроводе с сосредоточенными параметрами

Принципиальная схема простейшего контура гидравлическо контура имеет вид

Уравнения движения жидкости в трубопроводе со сосредоточенными параметрами.

Принципиальная схема простейшего контура гидравлического привода имеет такой вид:

рисунок 1

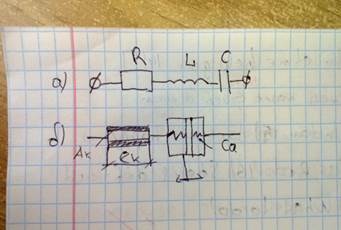
Уравнение электрические цепи может быть записано дельтаU=R_i+L*di/dt+1/c*интеграл(idt)                                           (1)

Падине давления на гидравлической цепи складывается из падений давления га гидравлическом аккумуляторе  и на капилляры.  Если допустить что участок на капилляре очень мал, скорость жидкости в сечении капилляра одинакова и равна среднему значению то потери на капилляре можно записать: дельтаР_кап=K_pq*Q_т+….  (2)

Потери давления на аккумуляторе пропорциональны перемещению поршня из нейтрали Х_а и обратно пропорциональны её площади: дельтаР=(С_а/A)*Х (3)

Перемещение поршня аккумулятора связана с расходом зависимостью:

dx/dt*A=Q=> dx_a=1/A*q/dt

дельтаР_а=с/A²*интеграл(Q/dt)   (4)

Т.о. падение давления на цепи с учётом уравнений 2 и 4 можно выразить уравнением: дельтаР=К*Р_pq*Q+L_k/A_k*dq/dt+c/A²*интеграл(Q/dt)

Сравнивая полученное уравнение с уравнением электрической цепи модно сделать заключение  в их полной идентичности. Поэтому уравнение 5 можно записать в ином виде: дельаР_цепи=R_r*Q+L_r*(dq/dt)+1/C_r**интеграл(Q/dt)  (6)

где К_к = Л_зйб Д_к=ро*L_k/A_k, C_r=L_k/C

Также модно доказать аналогичность электрических и пневматических цепей. Рассмотрим аналоги более распространённых электрических

элементов цепи их мат. описание сведя их в таблицу.

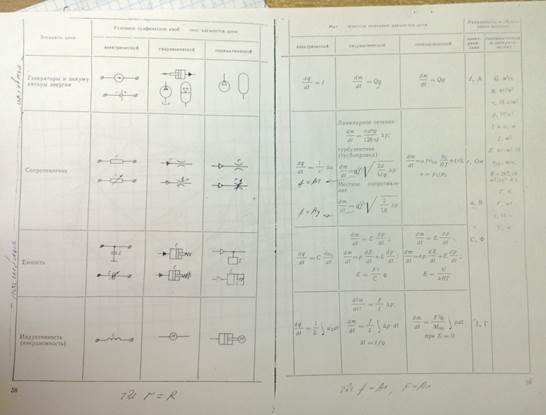
Аналогия топологических уравнений.

Как уже отмечалось топологические уравнения в большинстве систем базируются на уравнениях равновесия и непрерывности.

Электрическая система. Связь между отдельными элементами этой системы устанавливается на основе законов Кирхгофа. Уравнения первого закона устанавливает равенство 0 суммы токов в узлах схемы т.е. Сумма(от 1 до К)I_i=0.

Узлом цепи называют точку в которой сходятся 2 или более его ветви. Из уравнения второго закона Кирхгофа видно что сумма падений напряжений на элементах схемы при их обходе по произвольному контуру равна 0, т.е. Сумма(от 1 до n)U_j=0. Где U_j – падение напряжения на j ветви схемы входящей в контур.

Контуром цепи называется замкнутая последовательность ветвей в которой каждый из узлов встречается  более одного раза.

Гидравлическая  (пневматическая) система.

Аналогом первого закона Кирхгофа является уравнение баланса расхода для узлов: Сумма(от I до К)(dm/dt)_i=0, для жидкости если ро =const, то закон узлов запишется следующим образом Сумма(от I до К)Q_i=0.

Мгновенный массовый расход (объёмный) считается положительным если движение потока направлена к узлу и отрицательным если от узла: