Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 9

Из теоремы умножения получаем: .

Утверждения:

1)   и любое событие  из  независимо.

Доказательство:

Т.к. , то

2) Любые два несовместных события с ненулевыми вероятностями зависимы.

Доказательство:

,

С другой стороны предположим противное, что  и  независимы, тогда:

. Противоречие.  и  зависимы.

3) Если события  и  независимы, , , то они совместны.

Доказательство:

Предположим противное. События  и не совместные, , .

, .Противоречие. События  и  совместные.

Определение: События  называются независимыми в совокупности, если для любых  из них  выполняется соотношение:

Определение: Если соотношение выполнимо только при , то события называются попарно независимыми.

Замечание: Из независимости попарно не следует независимость совокупности.

Если событие  независимо в совокупности, то вероятность появления хотя бы одного из них считается по формуле:

Доказательство:

1)

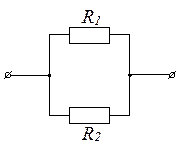
2)

 - вероятность работы - го элемента.

Вероятность работы:

Первая схема проводит ток, когда проводит ток хотя бы один элемент.

, где  - вероятность отказа первого элемента,  - вероятность отказа второго элемента.

Вторая сема проводит ток, когда оба элемента проводят ток.

Пример:

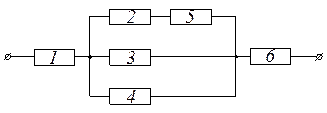
Первая ветвь (2-5): ,

Для параллельного блока:

Для всей цепи:

Пример: Новогодняя гирлянда содержит 20 лампочек. Вероятность перегорания одной лампочки 0,01. Найти вероятность того, что гирлянда будет работать.

 - для одной лампочки.

Формула полной вероятности.

Теорема (формула полной вероятности): Пусть событие  может произойти с одни и только с одним из не попарно совместных событий.

Т.е.  и  для , тогда существует формула:

Определение:  События  называются гипотезами.

Доказательство:

Пример: В цехе 20 станков, на которых 10 марки A, 6 марки B, 4 марки C. Вероятность того, что качество детали окажется отличным для станка марки A – 0,9, B – 0,8, C – 0,7. Найти вероятность того, что выпущенная цехом деталь отличного качества.

Событие ={выпущенная цехом деталь отличного качества}.

{Деталь со станка марки A}

{Деталь со станка марки B}

{Деталь со станка марки C}

 - вероятность того, что деталь выпущена станком марки A

 - вероятность того, что деталь выпущена станком марки B

 - вероятность того, что деталь выпущена станком марки C

 - вероятность того, что деталь отличного качества, при условии, что деталь со станка марки A

 - вероятность того, что деталь отличного качества, при условии, что деталь со станка марки B

 - вероятность того, что деталь отличного качества, при условии, что деталь со станка марки C

Теорема Байеса: Если выполнимо условие теоремы полной вероятности и , то имеет место формула Байеса:

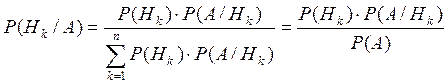
Замечание: Формула Байеса – единственная формула, которая дает апостериорно (после опыта) оценку вероятности гипотез.

Формулу Байеса применяют, когда событие уже произошло, для переоценки вероятности гипотез. 

Доказательство:

По теореме умножения верно равенство:

Пример: Число грузовых машин проезжающих по шоссе относится к числу легковых машин, как 3/2. Вероятность того, что будет заправляться грузовая машина 0,1, легковая – 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что подъехала грузовая машина.

={к бензоколонке подъехала машина}

={по шоссе едет грузовая машина}

={по шоссе едет легковая машина}

={вероятность того, что подъехала к бензоколонке машина, при условии, что она грузовая}

={вероятность того, что подъехала к бензоколонке машина, при условии, что она легковая}

={вероятность того, что ехала грузовая машина, при условии, что она подъехала на заправку}

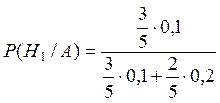
Повторение испытаний. Схема Бернулли.

Определение: Последовательные испытания называются независимыми, если вероятность осуществления любого исхода в -ом по счету испытание не зависит от реализации исхода в предыдущих испытаниях.