Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 19

Статистические оценки неизвестных параметров распределения.

Обычно вид закона распределения генеральной совокупности известен, но неизвестны параметры. Одна из задач статистики − нахождение оценок неизвестных параметров по выборке.

Пусть из генеральной совокупности с функцией распределения , где  − неизвестный параметр произведения выборки объемом . В качестве оценки параметра  рассматривают функции элемента выборки, которые называют статистикой.

Статистика:

Статистики являются случайными величинами . Задача оценки неизвестного параметра  сводится к нахождению статистики, которая может быть использована в качестве приближенного значения неизвестного параметра . Оценки параметров бывают точечными и интервальные.

Точечная оценка определяется одним числом.

Интервальной называют оценку, которая определяется двумя числами  и   − концами интервала покрывающего оцениваемый параметр.

Свойства точечных оценок.

Оценка  называется смещенной, если ее математическое ожидание равно оцениваемому параметру.

Разность  называется смещением оценки.

Оценка  называется состоятельной, если при увеличении объема , сходится по вероятности , т.е. для любого .

Пусть  и  две различные не смещенные оценки параметра .

Если , то  эффективней  оценки . Требование не смущенности устраняет систематические ошибки, обусловленные ограниченным объемом выборки.

Требование эффективности используется   в выборке оценки обладающей наименьшим разбросом.

Статистическая оценка математического ожидания.

Определение: выборочным средним  называется среднее арифметическое элементов выборки.

Для группированной выборки:

, где  − середины интервала группировки,  − частота попадания в интервал,  − количество интервалов группировки.

Замечание: Выборку  обычно рассматривают как реализацию случайной величины с независимыми компонентами. Причем каждая из компонент имеет распределение генеральной совокупности с теми же числовыми характеристиками.

Доказательство состоятельности:

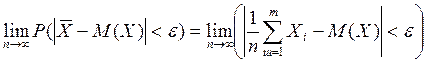
Пример: Пусть дан вариационный ряд:

Статистическая оценка дисперсии.

Определение: отклонением называется разность между элементом выборки и выборочным средним.

Теорема: Сумма произведения отклонений на соответствующие частоты равна 0.

Доказательство:

Следствие: Среднее значение отклонения равно 0.

Определение: Выборочной дисперсией называется величина , определяемая по формуле.

 − для статистической выборки.

Для группированной выборки:

Выборочная дисперсия является смещенной оценкой.

Определение: Направленной дисперсией  называется величина равная .

 является несмещенной оценкой дисперсии.

Общие методы нахождения точечных оценок.

1) Метод моментов

2) Метод максимального правдоподобия

Метод моментов:

Пусть известен вид распределения генеральной совокупности, но неизвестны параметры .

По выборке вычисляют   выбранных моментов и приравнивают их к соответствующим теоретическим моментам.

Начальный момент -го порядка считается по формуле:

Центральный момент -го порядка:

Замечание: Оценки математического ожидания и дисперсии получены с помощью метода моментов. К недостаткам метода моментов относится то, что оценки могут быть смещенными и необязательно эффективными.

Метод максимального правдоподобия:

Рассмотрим результаты выборки как реализацию -мерной случайной величины независимой компоненты. Для получения оценки неизвестного параметра , будем искать такое значение , при которой вероятность реализации этой выборки была бы максимальной.

Вероятность того, что при  независимых напряжений выборка  будет считаться по формуле:

Функция  называется функцией правдоподобия, а величина  - точка максимума этой функции являющаяся оценкой, полученной по методу максимального правдоподобия. (МП − оценка).