Математика \ Математика

Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 21

Определение: Статистической гипотезой называется любое предположение относительно параметров или вида распределения случайной величины .

Определение: Статистическая гипотеза называется односторонней, если она однозначно определяет распределение случайной величины . В противном случае гипотеза называется сложной.

Определение: Гипотеза называется параметрической, если вид распределения случайной величины известен, а по выборке надо сделать предположение о параметрах.

Наряду с выдвинутой гипотезой обычно рассматривают одну или несколько альтернативных или конкурирующих гипотез. Если выдвинутая гипотеза отвергается, то ее место занимает альтернативная.

Основную гипотезу называют нулевой .

Альтернативную гипотезу называют первой .

Задача проверки статистических гипотез состоит в том, чтобы сформулировать такое правило, которое позволило бы по результатам соответствующих наблюдений принять или отклонить гипотезу.

Правило, согласно которому проверяе5мая гипотеза применяется, называют статистическим критерием проверки гипотезы .

Дана случайная величина , ее выборка, сформулированная гипотеза .

Находят такую статистику характерную отклонению эмпирических данных от соответствующей гипотезы гипотетических данных, распределение которой в случае справедливости гипотезы можно было бы определить.

Величину называют статистикой критерия .

Пусть статистика при гипотезе известна.

Через обозначим множество значений статистики , − уровень значимости, такое подмножество , что при условии истинности гипотеза , вероятность попадания статистики в равно .

Пусть − выборочное значение статистики, тогда гипотеза отклоняется, если , и гипотеза принимается, если .

Определение: Критерий, который используют заранее заданную вероятность, называют критерием значимости.

Определение: Множество всех значений статистики критерия, при которых гипотеза отклоняется, называется критической областью.

Определение: Множество называют областью принятия гипотезы .

Схема проверки статистики гипотез:

1) Сформулировать проверяемую и альтернативную гипотезы.

2) Назначить уровень значимости .

3) Выбрать подходящую статистику критерия для проверки гипотезы .

4) Определить выборочное распределение статистики при условии, что гипотеза верна.

5) В зависимости от формулировки альтернативной гипотезы определить критическую область.

6) Получить выборку наблюдений и вычислить выборочное значение статистики критерия.

7) Если , гипотезу отклонить. Если же , гипотеза не противоречит результатам наблюдений.

Замечание: Значение может попасть в не потому, что неверна гипотеза , а из-за малого объема выборки и недостатков в методике проведения эксперимента.

Ошибку, совершаемую при отклонении правильной гипотезы , называют ошибкой первого рода. Вероятность ошибки первого рода равна уровню значимости .

Ошибка второго рода заключается в принятии гипотезы , если верна альтернативная гипотеза .

Вероятность ошибки второго рода считается по формуле:

При заданном , вероятность ошибки второго рода может быть уменьшена за счет увеличения объема выборки.

Если вероятность ошибки второго рода не должна превышать заданного значения , то объем выборки находят из системы:

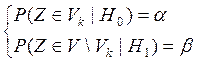
Статистическая проверка гипотезы о виде распределения генеральной совокупности.

Пусть выборка наблюдений случайной величины с неизвестной функцией распределения .

Гипотеза заключается в том, что . Выборочные данные группируют, разбивая множество значений случайной величины на непересекающихся интервалов числами .