Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 11

1)  − монотонно неубывающая функция, т.е. если , то .

Доказательство:

2) Вероятность функции

Вывод:  любой случайной величины есть не убывающая, непрерывная слева, и удовлетворяющая условиям  , ,  функция.

Обратное: Каждая неубывающая непрерывная слева, удовлетворяющая условию , ,  функция может быть рассмотрена, как функция распределения вероятностей.

Определение: Случайная величина  называется дискретной случайной величиной (ДСВ), если множество ее значений конечно и  , .

Определение: Законом распределения ДСВ называется перечень значений, которые принимает величина и соответствующая им вероятность. Закон распределения задается в виде таблицы называемой рядом распределения.

			…
			…

Пример: В урне 4 шара с номерами 1, 2, 3, 4. Извлекли 2 шара. Найти закон распределения суммы номеров извлеченных шаров.

3=1+2

4=1+3

5=2+3=1+4

6=2+4

7=3+4

 - число способов.

Вероятность каждого из способов равна .

Закон распределения:

	3	4	5	6	7

Определение: Закон распределения дискретной случайной величины (ДСВ) можно изобразить графически, для этого строят точки с координатами (). Полученная фигура называется многоугольником распределения.

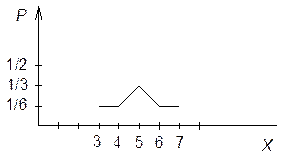
Некоторые законы распределения ДСВ.

1)  Биноминальное распределение:

Пусть производится  независимых испытаний, в каждом из которых  событие  может появиться и не появиться. Вероятность появления события  в одном испытании постоянно и равно . Дискретная случайная величина   - число появления события  в этих испытаниях.

   …

Биноминальным называется распределение вероятности определенной формулой Бернулли.

	0	1	2	3	…

Задача: Монета брошена 2 раза. Составить закон распределения случайной величины  числа появления герба.

, ,

	0	1	2

	0	1	2

2)  Распределение Пуассона:

Формула выражает закон распределения Пуассона, вероятности массовых () и редких () событий.

Определение:  Потоком событий называется последовательность событий, которая наступает в случайные моменты времени.

Потоки могут обладать следующими свойствами:

1) Свойство стационарности: Вероятность появления  событий на любом промежутке времени зависит только от числа  и от длительности  промежутка, и не зависит от начала отсчета.

2) Отсутствие последействия: Вероятность появления  событий на любом промежутке времени не зависит от того, появились или нет события в момент времени, предшествующих началу рассматриваемого промежутка.

3) Ординарность: За бесконечно малый промежуток времени может появиться не более одного события.

Определение: Простейшим или Пуассоновским

Называют поток событий, который обладает свойствами стационарности, ординарности и отсутствия последействия.

Определение: Интенсивностью потока  называют среднее число событий, которое происходит в единицу времени.

Если интенсивность потока   постоянна и не известна, то вероятность появления  событий за время  определяется формулой:

1)  Стандартность очевидна, т.к.   зависит только от  и .

2)  Формула не использует информацию о появлении события до рассматриваемого промежутка, то отсутствие последействия очевидно.

3) 

Величина  при  пренебрежительно мала, т.е. свойство ординарности имеет место.