Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 12

Пример: Среднее число вызовов такси поступающих на диспетчерский пункт в одну минуту равно 3. Найти вероятность того, что в течении 4 минут поступит:

а) 2 вызова б) менее двух вызовов.

а) , 

б)

3) Геометрическое распределение:

Производится независимые испытания, в каждом из которых вероятность появления события  равна . Испытания заканчиваются как только появится событие . Дискретная случайная величина   - число испытаний, которое надо провести до появления события .

Вероятность того, что  в предыдущем событии не появилось, а в следующем появилось

	1	2	3	…

Т.к. , то  (свойство выполняется)

Пример: Производится стрельба по цели до первого попадания. Вероятность попадания при одном выстреле 0,3. Составить закон распределения ДСВ  - число выстрелов, которое надо произвести до первого попадания.

	1	2	3	…
	0,3

4) Гипергеометрическое распределение:

Пусть  - число изделий,  - стандартных. Отбирают  изделий. Определить вероятность того, что среди них  стандартных. ДСВ  - число стандартных изделий среди  отобранных.

Эта формула определяет распределение, называемое гипергеометрическим.

	0	1	2	…
				…

Пример: В партии 5 изделий, из которых 3 стандартных. На удачу отбирают 2 изделия. Написать закон распределения числа стандартных изделий из отобранных.

	0	1	2

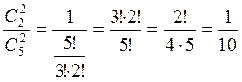
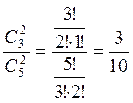
Пример: Для данного распределения построить многоугольник распределения и функцию распределения вероятности.

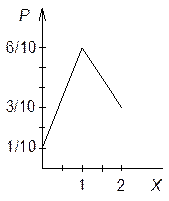
 - функция непрерывная слева.

1)  

2)  

3)  

4)  

Непрерывные случайные величины

Определение: Случайную величину называют непрерывной случайной величиной, если ее функция распределения  есть непрерывная кусочно-дифференцируемая  функция с непрерывной производной.

Определение: Средней плотностью распределения вероятности называется величина .

Определение: Если существует предел средней плотности вероятности при , то он называется плотностью распределения вероятности в точке .

Обратное:

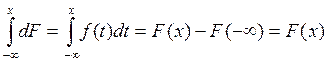
Свойства функции :

1)  

Т.к.  монотонно неубывающая функция, то ее производная   не отрицательна.

2)

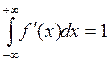
Замечание:

1) Любая функция являющаяся неотрицательной и обладающая свойством нормировки может быть областью распределения некоторой случайной величины.

2) Для непрерывной случайной величины вероятность попасть в точку равна 0.

3)

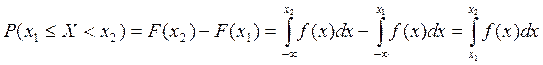
1) Первое свойство говорит о том, что функция неотрицательна.

2) Второе свойство показывает, что вся заштрихованная площадь равна 1.

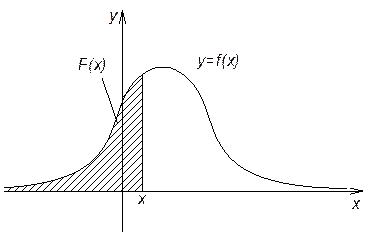
3)

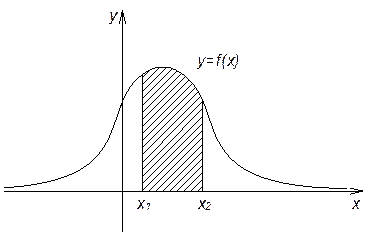
Равномерное распределение.

Определение: Случайная величина  называется равномерно распределенной на отрезке , если ее плотность распределения вероятности на данном отрезке:

Нахождение константы:

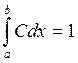
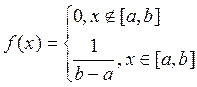
Нахождение :

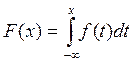
1)  

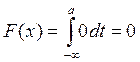
2)  

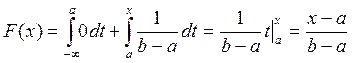
3)  

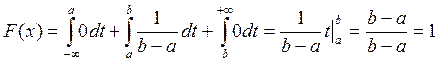
Показательное распределение

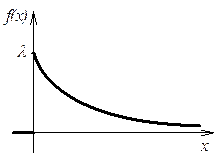
Определение: Непрерывная случайная величина называется распределенной по показательному закону параметром , если ее плотность распределения вероятности задается формулой:

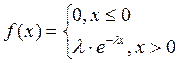
Нахождение :

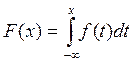
1)  

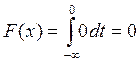
2) 

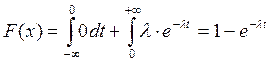
Числовые характеристики случайных величин

Определение: Математическим ожиданием называется действительное число, определенное формулой:

Математическое ожидание существует, если ряд для ДСВ или интеграл для НСВ сходится.

Свойства:

1) Если , то

Доказательство:

2)

Константу можно выносить за знак математического ожидания.

Доказательство: