Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 8

Определение: Число называется вероятностью события .

1) Если событие невозможно, то ,

2) Если событие достоверно, то

3) Для любого события

Доказательство:

Т.к. , то

Аксиоматические определения вероятности.

Пусть - произвольное пространство элементарных событий. Система подмножеств называется алгеброй событий, если выполнимы условия:

2) , ,

Определение: Вероятностью называется числовая функция, определенная для всех из и удовлетворяющая условию:

1) - аксиома не отрицательности

2) - аксиома нормировки

3) если и не совместны, то - аксиома конечной адитивности

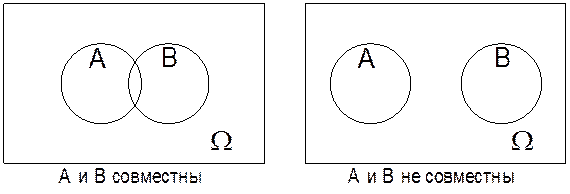
Следствия из аксиом:

Доказательство:

Возьмем все пространство . Тогда .

Доказательство

3) Если влечет за собой (), то

Доказательство

, ,

4) Если события совместные, то

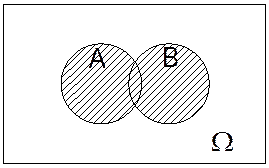
Вычтем из первого уравнения второе.

Следствия из теоремы сложения:

Для любых двух событий и :

5) Пусть события образуют полную группу событий, т.е. они не совместны и их сумма равна всему пространству . Тогда .

Доказательство:

Посчитаем в формуле вероятность левой и правой части.

Подходы:

1) Статистический

2) Аксиоматический

3) Классический

4) Геометрический

Классическое определение вероятности:

Пусть все пространство

, где - число экспериментов.

Любое событие .Тогда , т.к. простые исходы не совместны, то: .

Определение: Элементарные события, составляющие событие называется исходами, благоприятствующими событию .

Определение: Вероятность события равна отношению числа исходов благоприятствующих событию к общему числу исходов.

Пример: Бросаются два игральных кубика. Определить вероятности следующих событий:

={Сумма выпавших очков меньше 7}

={Произведение выпавших очков меньше 7}

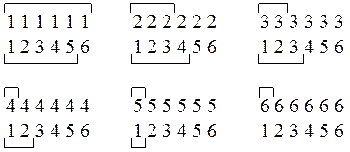
Пример: В урне 10 шаров, 3 черных и 7 белых. Вынимаются 3 шара. Найти вероятность того, что среди трех вынутых два белых.

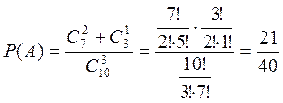
Геометрическое определение вероятности.

Пусть некоторая область плоскости или прямой или пространства. Событие состоит в том, что точка, брошенная на плоскость, попадает в область под . Причем попадание в является достоверным событием, а площадь плоскости является конечной величиной.

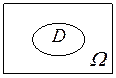
В каждой точке области ставится в соответствии элементарное событие попадания в эту область.

Теорема: Пусть вероятность попадания в любую область из пропорционально площади области и не зависит от места расположения в и формы области , тогда:

равно отношению площади области к площади области .

Доказательство:

По условию . Найдем коэффициент пропорциональности:

Пример: Два студента договорились встретиться в промежуток времени с часу до двух. Приход студентов в любой момент времени равновероятен. Первый приходит, ждет второго 15 минут и уходит. Какова вероятность того, что они встретятся.

- время прихода первого студента

- время прихода второго студента

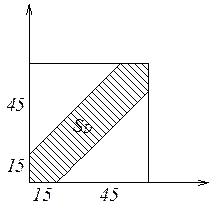
Пример: В любой момент времени промежутка равновозможно поступление двух сигналов. Оба сигнала будут приняты, если разность моментов поступления сигналов больше . Какова вероятность того, что оба сигнала будут приняты?

- скорость поступления первого сигнала

- скорость поступления второго сигнала

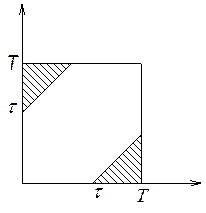
Условная вероятность.

Определение: Условной вероятностью события по отношению к событию называется вероятность осуществления события , определенное в предположении, что событие уже произошло.

В классической вероятностной схеме найдем условную вероятность.

Пусть состоит из несовместных равновозможных исходов.