Пусть
производится ![]() независимых испытаний, в каждом из
которых может появиться или не появиться событие
независимых испытаний, в каждом из
которых может появиться или не появиться событие ![]() .
Появление события
.
Появление события ![]() в одном испытании называется
успехом, не появление – неуспехом. Вероятность появления события
в одном испытании называется
успехом, не появление – неуспехом. Вероятность появления события ![]() в одном испытании -
в одном испытании - ![]() , а вероятность неуспеха -
, а вероятность неуспеха - ![]() . Найти вероятность того, что событие
. Найти вероятность того, что событие ![]() в
в ![]() испытаниях
появиться ровно
испытаниях
появиться ровно ![]() раз.
раз.
Вероятность
одного сложного события заключающегося в том, что в ![]() испытаниях
событие
испытаниях
событие ![]() наступит
наступит ![]() раз,
и не наступит
раз,
и не наступит ![]() раз, по теореме умножения
независимых событий равна:
раз, по теореме умножения
независимых событий равна:
![]()
Число сложных
событий есть число сочетаний ![]() , и они не совместны.
Тогда вероятность наступления события
, и они не совместны.
Тогда вероятность наступления события ![]()
![]() раз.
раз.
![]() - формула Бернулли.
- формула Бернулли.
Пример: Вероятность перерасхода энергии в течение суток 0,2. Найти вероятность того, что в течении ближайшей недели перерасход наступит в течении двух суток.
![]()
Наивероятнейшее число успехов в последовательности независимых испытаний.
Пусть ![]() ,
, ![]() .
.
Исследуем ![]() как функцию от аргумента
как функцию от аргумента ![]() . Для этого выпишем:
. Для этого выпишем:
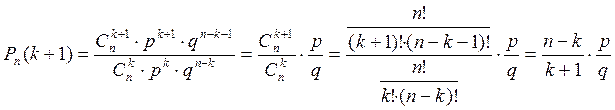
![]()
![]()
![]()
![]()
Т.е. функция ![]() возрастает при переходе от
возрастает при переходе от ![]() к
к ![]() , если
, если
![]() , и убывает, если
, и убывает, если ![]() ,
а также остается неизменной, если
,
а также остается неизменной, если ![]() . Следовательно,
наивероятнейшее число успехов
. Следовательно,
наивероятнейшее число успехов ![]() должно удовлетворять
неравенству:
должно удовлетворять
неравенству:
![]() , т.к.
, т.к. ![]() , то:
, то:
![]()
Если число ![]() целое, то наивероятнейшее число
целое, то наивероятнейшее число ![]() может иметь два значения:
может иметь два значения: ![]() и
и ![]() . Если
же
. Если
же ![]() − дробь, то вероятность
− дробь, то вероятность ![]() не возрастает не при каких
не возрастает не при каких ![]() и вероятнее всего, что в
и вероятнее всего, что в ![]() испытаний не будет ни одного успеха.
испытаний не будет ни одного успеха.
Пример: Испытываются 15 элементов некоторого устройства. Вероятность, того что элемент выдержит испытание 0,9. Найти наивероятнейшее число элементов выдержавших испытание и соответствующую вероятность.
![]() ;
; ![]() ;
; ![]() .
.
![]()
![]()
Вероятнее всего 14 элементов выдержат испытание.
![]()
Локальная теорема Лапласа:
Если вероятность появления событий в каждом испытании постоянна и отлична от 0 и 1,то:
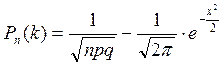 , где
, где ![]()
Замечание:
Функция 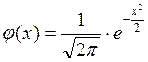 затабулирована и является четной
функцией.
затабулирована и является четной
функцией.
Пример: Найти
вероятность того, что событие ![]() наступит 80 раз в 400
испытаниях, если вероятность появления события в одном испытании 0,2.
наступит 80 раз в 400
испытаниях, если вероятность появления события в одном испытании 0,2.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]()
![]()
![]()
Интегральная теорема Лапласа.
Производится ![]() независимых испытаний. Найти вероятность
того, что событие
независимых испытаний. Найти вероятность
того, что событие ![]() появится не менее
появится не менее ![]() и не более
и не более ![]() раз,
если вероятность появления события
раз,
если вероятность появления события ![]() в одном испытании
постоянно и равно
в одном испытании
постоянно и равно ![]() .
.
Теорема:
Если вероятность появления события ![]() в каждом испытании
постоянно и отлично от 0 и 1, то:
в каждом испытании
постоянно и отлично от 0 и 1, то:
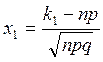 ;
; 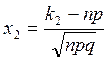 ;
;
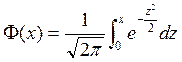
![]()
Пример: Вероятность того, что деталь бракованная – 0,2. Найти вероятность того, что среди 400 просматриваемых деталей бракованными окажутся от 70 до 100 деталей.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
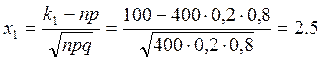
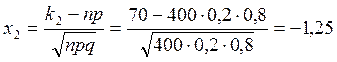
![]()
Формула Пуассона.
Постановка
задачи: Найти вероятность того, что при очень большом числе испытаний, в
каждом из которых вероятность появления события ![]() очень
мала, если событие
очень
мала, если событие ![]() наступит ровно
наступит ровно ![]() раз.
раз.
![]() -велико;
-велико; ![]() -
мало.
-
мало.
![]()
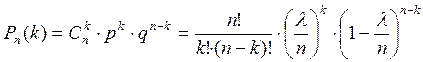
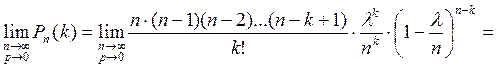
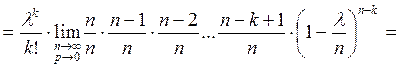
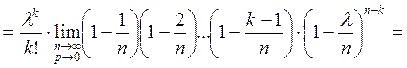
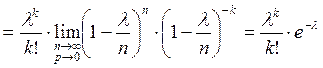 − формула Пуассона.
− формула Пуассона.
Пример: Завод отправил 2000 изделий. Вероятность повреждения изучения в пути равно 0,001. Найти вероятность того, что на базу прибудут ровно три бракованных изделия.
![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]()
Случайные величины.
Определение: Случайной называется величина, которая в результате испытаний принимает одно и только одно возможное значение, наперед неизвестное и зависящая от случайных величин.
Определение:
Числовая функция, определенная на ![]() называется случайной
величиной
называется случайной
величиной ![]() .
.
Каждому
элементарному событию ![]() ставится в соответствии число
ставится в соответствии число ![]() , т.е. если в результате испытаний
появляется элементарное событие
, т.е. если в результате испытаний
появляется элементарное событие ![]() , то случайная
величина
, то случайная
величина ![]() принимает значение
принимает значение ![]() .
.
Рассматриваются
только те случайные величины, до которых определена вероятность того, что
случайная величина примет значение меньшее ![]() .
.
Определение:
Функция распределения вероятностей случайной величины ![]() называется
действительной переменной
называется
действительной переменной ![]() , определяющаяся
формулой:
, определяющаяся
формулой:
![]()
Т.к. ![]() − вероятность, то
− вероятность, то ![]() .
.
Справедливо следующее равенство:
![]()
![]()
![]()
Замечание:
Функция ![]() считается непрерывной слева.
считается непрерывной слева.
Свойства
функции ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.