Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 14

 - функция распределения вероятности ненормированного нормального закона.

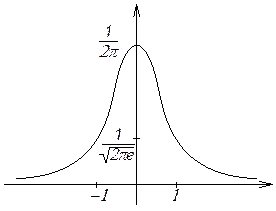
Вероятность попадания в интервал. Правило трех .

Считаем, что случайная величина отклонилась.

Пусть :

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратичного отклонения.

Многомерные случайные величины.

Определение: Пусть случайные величины:

Вектор  называется случайным вектором или -мерной случайной величиной.

 называется координатой или компонентой случайного вектора .

Функция , где  - некоторое число, называется -мерной функцией распределения случайного вектора  или совместной функцией распределения случайных величин.

Функция распределения двумерного случайного вектора.

Определение: Функцией  распределения двумерного случайного вектора называется функция .

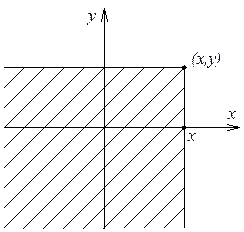
Свойства:

1)  являются неубывающей функцией по обоим аргументам, т.е. при  , при  

Доказательство:

                                                    

,

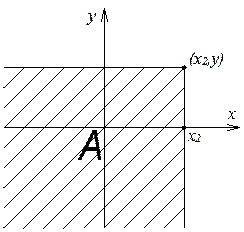
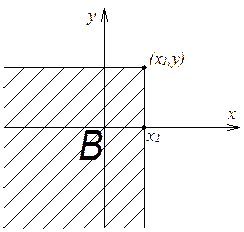
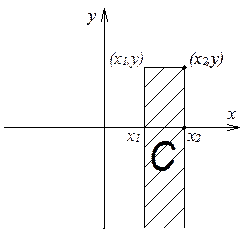
2) Функция непрерывна слева по каждому аргументу.

Доказательство:

Зафиксируем . Пусть , тогда  это есть функция распределения вероятности случайной величины  и она непрерывна слева. Аналогично по .

3)

Доказательство:

а) - такое событие не возможно, следовательно, вероятность равна нулю.

б) - такое событие не возможно, следовательно, вероятность равна нулю.

в) - такое событие достоверно, следовательно, вероятность равна 1.

4) Вероятность того, что случайная величина  попадает в интервал

Доказательство:

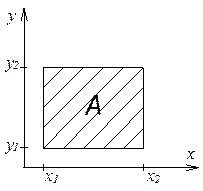
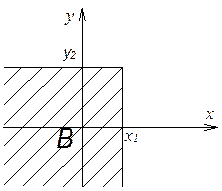
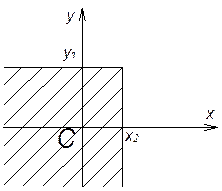
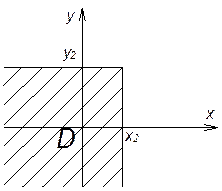
5)

Доказательство:

Рассмотрим событие

Причем события под знаком суммы попарно не совместно.

.

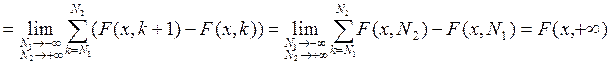Дискретные двумерные случайные векторы.

Определение: Двумерный случайный вектор называется дискретным, если каждая его компонента является дискретной случайной величиной.

Множество всех возможных значений дискретного двумерного случайного вектора не более счетного.

Определение: Законом распределения дискретного случайного вектора называется перечень всех возможных значений пар компонентов и соответствующая каждой паре вероятность.

Закон распределения задается таблицей:

			…
…

Законы распределения компонент получают из законов распределения векторов следующим образом:

Пример:

	2	4	6
1	0,08	0,3	0,02
2	0,2	0,3	0,1

	2	4	6
	0,28	0,6	0,12

	1	2
	0,4	0,6

	0	0	0	0
	0	0,08	0,38	0,4
	0	0,28	0,88	1

Непрерывный двумерный случайный метод.

Определение: Двумерный случайный вектор называется  случайным вектором, если функция распределения непрерывна на всей области, и  существует такая неотрицательная интегрируемая в бесконечных пределах по каждой из координат функция , что:

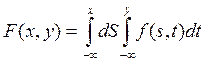
Функция  называется плотностью распределения вероятности случайного вектора.