Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 7

Теорема: Число различных размещений с повторениями из  элементов по  элементам определяется по формуле:

Пример: Десять шариков случайным образом рассылаются по семи лункам.

Перестановки с повторениями.

Определение: Перестановкой с повторениями из  элементов называется  любое упорядочение конечного множества , состоящее из элементов среди которых есть совпадающие.

Теорема: Пусть множество  состоит из  элементов, причем различными являются элементы  и элементы  представлен в  экземплярах,  представлен в  экземплярах,  −  в   экземплярах. Тогда число различных перестановок определяется формулой:

Пример: Дано слово «балалайка». Найти число различных перестановок.

б-1, а-4, л-2, й-1, к-1.

Число различных перестановок:

Сочетания с повторениями.

Определение: Сочетание с повторениями из  элементов по  элементам называется всякое подмножество множества , состоящее из  элементов, причем элементы подмножества не обязательно должны быть различными.

Замечание: Сочетания с повторением является неупорядоченным подмножеством.

Теорема: число возможных сочетаний с повторениями из  элементов по  элементам определяется формулой:

ТЕОРИЯ ВЕРОЯТНОСТИ.

События. Операции над событиями.

Определение: Под экспериментом понимают осуществление комплексов условий сопровождающихся регистрацией результата.

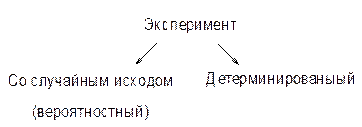
Определение: Эксперимент называется детерминированным, если результат эксперимента предсказуем на основе естественного закона.

Определение: Различные исходы случайного эксперимента называется элементарными событиями, а множество всех исходов называется пространством элементарных событий.

Пример:

1) Бросание монеты

Элементарных исходов два:

={выпадение герба}

={выпадение решки}

Все пространство элементарных событий состоит из двух элементарных событий.

2) Бросание игральной кости

={выпадение 1}

={выпадение 2}

={выпадение 3}

={выпадение 4}

={выпадение 5}

={выпадение 6}

Определение: Случайным событием называется всякое подмножество пространства элементарных событий.

 - выпадение нечетного числа очков.

Определение: Невозможным называется событие, которое не может произойти в результате эксперимента.

Определение: Достоверным называется событие, которое всегда происходит в результате эксперимента.

Пример: Невозможным является событие выпадения отрицательного числа очков. Достоверным является событие выпадения числа большего 0, но меньшего 6.

Невозможное событие совпадает с Æ, а достоверное событие совпадает со всем пространством элементарных событий.

Определение: События  и  называются равными (), если они состоят из одних и тех же элементарных событий.

Определение: Событие  есть следствие события , если  содержит все элементарные события, входящие в , т.е. если  происходит всякий раз, тогда происходит .

Определение: Суммой  событий  и  называется событие, которое состоит из всех элементарных событий принадлежащих хотя бы одному из событий  или .

Определение: Произведение  событий  и  называется событие, состоящее из элементарных событий, принадлежащих и  и .

Определение: Разностью  событий  и  называется событие , состоящее из элементарных событий принадлежащих и не принадлежащих .

Определение: Событие  называется противоположным событию , т.е. .

Диаграмма Эйлера- Венна для событий:

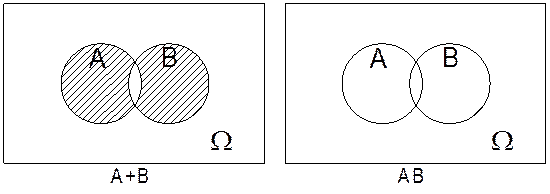
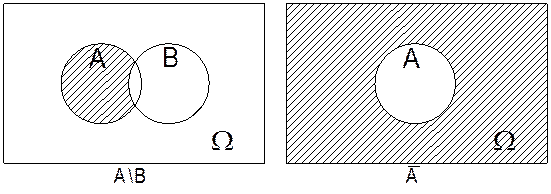
Свойства:

1)

2)

3)

4)

5)

6)

7)

8)

9)

Частота. Статистические определения вероятности.

Пусть некоторый эксперимент осуществляется  раз.

Определение: Относительной частотой осуществления события  в серии из  испытаний называется отношение числа испытаний, в которых появилось событие  к числу  всех испытаний.

.

Определение: Если многократно повторять серии из  опытов, то относительная частота  будет меняться от серии к серии. Но по мере увеличения числа повторных испытаний, относительная частота стабилизируется около некоторого постоянного и неслучайного для данного события  в данном эксперименте значения . Это свойство называется свойством устойчивости относительной частоты.