Вероятностный
смысл: ![]() есть предел отношения вероятности
попадания случайной точки в прямоугольник со сторонами
есть предел отношения вероятности
попадания случайной точки в прямоугольник со сторонами ![]() и
и![]() к площади этого прямоугольника, когда
стороны стремятся к нулю.
к площади этого прямоугольника, когда
стороны стремятся к нулю.
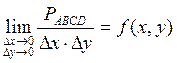
Свойства плотности:
1) ![]()
2) ![]()
Свойство
следует из того, что ![]() есть неубывающая функция своих
аргументов.
есть неубывающая функция своих
аргументов.
3) Свойство нормировки:
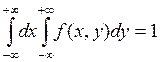
По свойству 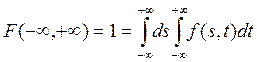
4)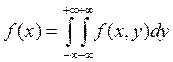
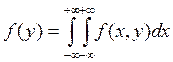
Плотности распределения вероятностей отдельных компонентов случайного вектора выражаются виде интегралов от совместных плотностей распределения.
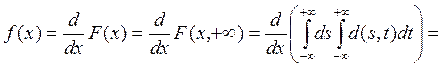
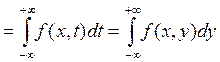
5) Если ![]() двумерный случайный непрерывный вектор,
то вероятность попадания случайной точки а произвольную область
двумерный случайный непрерывный вектор,
то вероятность попадания случайной точки а произвольную область ![]() определяется формулой:
определяется формулой:
![]()
Доказательство:
![]()
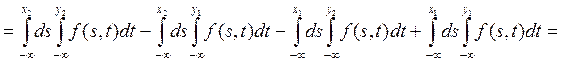
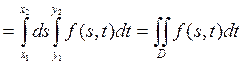
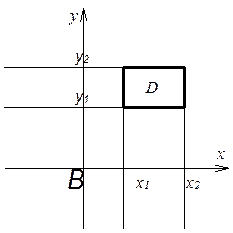
В общем
случае область ![]() апроксимируется объединением
вписанных и описанных прямоугольников. При стремлении сторон прямоугольника к
нулю получается требуемая формула.
апроксимируется объединением
вписанных и описанных прямоугольников. При стремлении сторон прямоугольника к
нулю получается требуемая формула.
Независимость случайных величин.
Определение:
Случайные величины ![]() называются независимыми, если
для любых событий
называются независимыми, если
для любых событий ![]() , где
, где ![]() -
подмножество числовой прямой, имеет место равенство:
-
подмножество числовой прямой, имеет место равенство:
![]() .
.
Теорема:
Случайные величины ![]() независимы тогда и только
тогда, когда в любой точке
независимы тогда и только
тогда, когда в любой точке ![]() с координатами
с координатами ![]() имеет место равенство:
имеет место равенство:
![]() (1)
(1)
Доказательство:
![]() (2)
(2)
За ![]() и
и ![]() выберем
любые полуинтервала числовой прямой.
выберем
любые полуинтервала числовой прямой.
![]() ,
,![]() .
.
Достаточность: Пусть условие (2) выполнено.
![]()
![]()
![]()
![]()
Необходимость: Пусть выполнены условия определения т.е. вероятность того, что
![]()
Устремим ![]() ,
,![]() к
к ![]() . Получим:
. Получим:
![]() что и требовалось доказать.
что и требовалось доказать.
Следствия:
1) Пусть ![]() плотность распределения вероятности
двумерного непрерывного случайного вектора. Случайные величины
плотность распределения вероятности
двумерного непрерывного случайного вектора. Случайные величины ![]() и
и ![]() независимы
тогда и только тогда, когда во всех точках непрерывности функции имеет место
равенство:
независимы
тогда и только тогда, когда во всех точках непрерывности функции имеет место
равенство: ![]() .
.
Доказательство:
Формулу (2)
дважды продифференцируем по ![]() и
и ![]() , и получим требуемое равенство.
, и получим требуемое равенство.
2) Для того что бы дискретные случайные величины были независимы необходимо и достаточно следующее равенство:
![]()
Условные законы распределения составляющих.
Определение:
Условным законом распределения составляющей ![]() при
при ![]() называют совокупностью условных
вероятностей:
называют совокупностью условных
вероятностей:
![]()
вычисленных в
предположении, что событие ![]() уже наступило.
уже наступило.
![]()
![]() .
.
Следовательно
условный закон распределения составляющей ![]() в
предположении, что событие
в
предположении, что событие ![]() уже наступило, имеет
вид:
уже наступило, имеет
вид:
![]() .
.
Теорема: Сумма вероятностей условного закона распределения равна единице.
Доказательство:
![]()
![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Пример: Найти
закон распределения ![]() при условии, что
при условии, что ![]() ,
, ![]() и
математическое
и
математическое ![]() .
.
|
|
1 |
3 |
4 |
|
1 |
0,15 |
0,1 |
0,25 |
|
2 |
0,3 |
0,1 |
0,1 |
![]()
|
|
1 |
3 |
4 |
|
|
|
|
|
![]()
Определение:
Условной плотностью распределения составляющей ![]() при
заданном значении
при
заданном значении ![]() называется отношение плотности
совместного распределения к плотности распределения составляющей
называется отношение плотности
совместного распределения к плотности распределения составляющей ![]() .
.
![]()
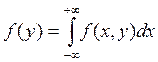
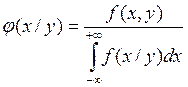
Все свойства распределения вероятностей остаются в силе:
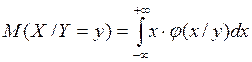 - условное математическое ожидание
- условное математическое ожидание
Пусть
случайные величины ![]() и
и ![]() независимы.
независимы.
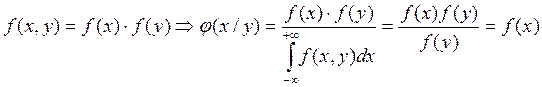 .
.
Если
компонента ![]() и
и ![]() независимы,
то условная плотность распределения равна безусловной плотности распределения.
независимы,
то условная плотность распределения равна безусловной плотности распределения.
![]()
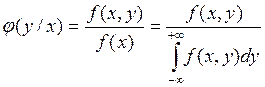
Числовые характеристики случайных величин.
Теорема:
Если случайные величины ![]() и
и ![]() независимы, то
независимы, то ![]() .
.
![]() .
.
![]()
![]()
![]() , т.к.:
, т.к.:
![]()
![]() .
.
Замечание:
Это свойство распространяется на сумму ![]() независимых
случайных величин.
независимых
случайных величин.
Математическое
ожидание и дисперсия ![]() -мерного случайного вектора.
-мерного случайного вектора.
Определение:
Математическим ожиданием ![]() -мерного случайного
вектора называется вектор составленный из математических ожиданий координат.
-мерного случайного
вектора называется вектор составленный из математических ожиданий координат.
![]() .
.
Определение:
Дисперсией ![]() - мерного случайного вектора
- мерного случайного вектора ![]() называется вектор составленный из дисперсии
координат.
называется вектор составленный из дисперсии
координат.
![]()
![]()
![]()
Для непрерывного:
![]()
![]()
Ковариация. Коэффициент корреляции.
Определение:
Ковариация случайных величин ![]() и
и ![]() называется число, определяемое формулой:
называется число, определяемое формулой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.