Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 5

2)  Сжатие по столбцам или строкам:

Из матрицы вычеркивают строку, которая полностью покрывается другой строкой и столбец, в который полностью входит какой-нибудь другой столбец.

3)  Соединяют ставшиеся в матрице импликанты и существенные импликанты знаком дизъюнкции и получают минимальную ДНФ.

Пример: Булева функция задана в СДНФ. Минимизировать ее.

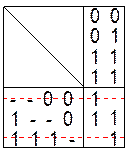
Каждая элементарная конъюнкция представляется двоичным набором, причем «0» пишем, если  входит с отрицанием, «1» - если без отрицания и знак «-», если не входит в конъюнкцию.

Разделяем наборы на классы с одинаковым числом «1».

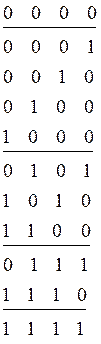
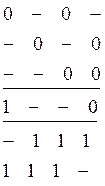
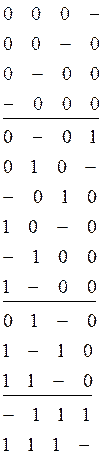
Сравниваем наборы из смежных классов и склеиваем их по правилу склеивания.

Сокращенная ДНФ:

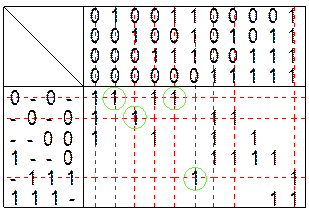
Ядро Квайна: ; ;  

Минимальная функция:

Геометрическая минимизация булевых функций

Пример: Изобразить геометрически

							СДНФ
л	л	л	и	и	л	и	000
л	л	и	л	и	л	л
л	и	л	и	и	л	и	010
и	л	л	и	л	и	и	100
л	и	и	л	и	л	л
и	л	и	л	л	и	и	101
и	и	л	и	и	л	и	110
и	и	и	л	и	л	л

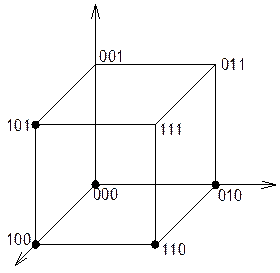
Через  обозначим все n-мерных наборов состоящих из «0» и «1».

Определение: Множество называется n-мерным кубом, а фиксированный набор  - его вершины.

Определение: Пусть  - фиксированные числа. Множество вершин куба таких, что ; ;… называется -мерной гранью.

- нижняя грань куба, r=1 (т.к. одна фиксированная координата).

 - двумерная грань

 r=2

 - одномерная грань (ребро).

Грани:

Определение: Геометрический способ задания булевой функции это задание множества вершин, в которой функция равна 1.

Пример: Булева функция задана геометрически. Получить ее запись в СДНФ и таблице.

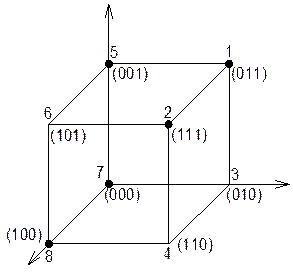
- СДНФ

0	0	0	1
0	0	1	1
0	1	0	0
1	0	0	1
0	1	1	1
1	0	1	0
1	1	0	0
1	1	1	1

Элементарная конъюнкция

Если ,

Через обозначают множество вершин соответствующих конъюнкции .

Число называется рангом конъюнкции.

            - одномерная грань

            - одномерная грань

                 - двумерная грань

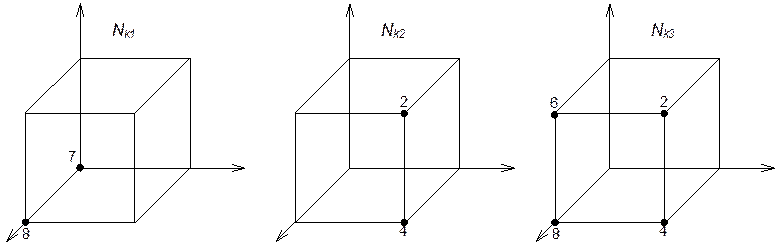
Замечания: Если булева функция , то множество , тогда ,

Определение: Пусть  и . Тогда число  называется рангом покрытия.

Геометрическая задача минимизации булевой функции принимает следующую формулировку: для данного множества  найти такое его покрытие гранями, чтобы ранг покрытия был наименьшим.

Алгоритм.

1)  Нанести множество  на трехмерный куб, для чего использовать или табличное задание функции, отметив на кубе вершины, в которых функция равна «1» или СДНФ, когда каждой простой конъюнкции входящей в СДНФ поставить в соответствии вершину.

2)  Если отмеченными окажутся все вершины куба, то данная функция тождественно истинна и не минимизируется.

3)  Если отмечены вершины какой-либо грани, то заменить все четыре вершины одной переменой названием грани.