Математика \ Математика

Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 17

1) Семейство законов распределения описываемых плотностью распределения , где − фиксированная плотность распределения вероятностей и также является видом распределения

2) Линейное преобразование не имеет вида распределения.

Теорема: Если случайные величины и независимы и − произвольные функции, то величины , тоже независимы.

Теорема: Пусть − ДСВ принимающая значения с вероятностью и , где − неслучайная функция.

, если ряд стоящий справа абсолютно сходится.

Теорема: Пусть − непрерывная случайная величина, имеющая плотность распределения вероятностей , , где неслучайная функция. Тогда:

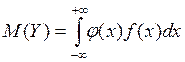, если интеграл абсолютно сходится.

Законы больших чисел.

Определение: Последовательность случайных величин называют сходящейся по вероятности при по случайной величине , если .

Т.е. каково бы не было число , найдется такое число , что для любого вероятность выполнения неравенства будет сколь угодно мала.

Теорема Чебышева: Пусть последовательность попарно независимых случайных величин, дисперсия которых ограничена в совокупности.

Тогда

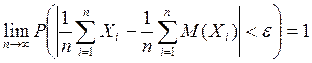
Теорема: Если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение близкое к нормальному.

Теорема Бернулли: Относительная частота успехов в независимых испытаниях по схеме Бернулли сходится по вероятности при вероятности успехов в одном испытании.

Замечание: Из теоремы не следует, что , т.к. в теореме идет речь о сходимости по вероятности.

Распределение .

Пусть нормальные независимые случайные величины с математическим ожиданием , . Тогда сумма квадратов распределены по закону с числом степеней свободы . Если же эти величины связаны между собой одним линейным соотношением, то число степеней свободы .

Функция распределения 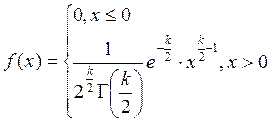, где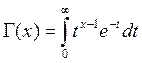

Распределение определяется одним параметром − числом степеней свободы и медленно приближается к нормальному при .

Распределение Стьюдента.

Пусть случайная величина распределена нормально с параметрами , , а случайная величина распределена по закону с степенями свободы.

Тогда величина 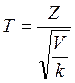имеет распределение Стьюдента с степенями свободы. С возрастанием распределения Стьюдента быстро приближается к нормальным.

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Определение: Математической статистикой называется наука основывающая на методах теории вероятности и заканчивающаяся систематизацией и отработкой экспериментальных данных.

Определение: Пусть рассматривается некоторый случайный эксперимент, связанный с случайной величиной . Полный набор всех возможных измерений случайной величины в этом эксперименте называется генеральной совокупностью.

Определение: Число членов образующих генеральную совокупность называется ее объемом. Объем генеральной совокупности может быть как конечным, так и бесконечным.

Определение: выборкой или выборочной совокупностью объема из генеральной совокупности называют последовательность наблюдаемых значений случайной величины соответствующих независимым повторений экспериментов.

Определение: Метод, состоящий в том, что на основании изучения характеристик и свойств выборок дается заключение о числовых характеристиках и законе распределения случайной величины называется выборочным методом.

Определение: Вариационным рядом выборки называют способ ее записи, при котором элементы упорядочиваются по величине.