Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 6

4)  Если отмечены вершины какого-либо ребра, то заменить вершины названием ребра.

Чтобы получить минимизированную форму надо выбирать ребра так, чтобы меньшим числом ребер покрыть все отмеченные вершины.

Пример: Булева функция задана таблично. Минимизировать ее геометрически.

0	0	0	1
0	0	1	0
0	1	0	0
1	0	0	1
0	1	1	0
1	0	1	1
1	1	0	1
1	1	1	1

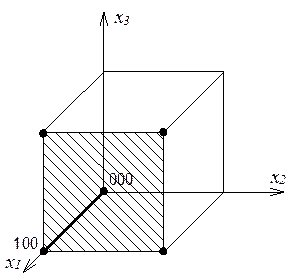
Получаем .

Минимизация с помощью карты Карно.

Пример:

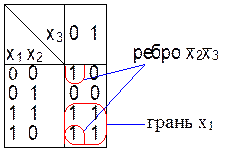
Получаем 

Замечание: Если булева функция зависит от четырех аргументов, то с помощью карты Карно находят четвертую переменную.

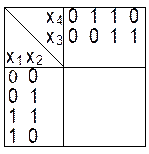
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

В комбинаторике есть два основных принципа:

1)  принцип сложения

2)  принцип умножения

Принцип сложения.

Пусть множество  состоит из  элементов , а множество  из  элементов , причем ни один из элементов множества  не совпадает ни с одним из элементов множества .

Выбрать один  элемент из множества  можно  различными способами, а из множества  различными способами. Тогда один элемент из множества  или  можно выбрать  различными способами.

Принцип умножения.

Пусть множество  состоит из  различных элементов , а множество  из  различных элементов .

Тогда множество  содержит  различных элементов.

Если первое действие можно выполнить  различными способами, а второе  различными способами, то оба действия могут быть выполнены  различными способами.

Определение: Конечное множество, состоящее из  элементов, называется упорядоченным, если его элементы каким-либо образом занумерованы числами .

Замечания:

1)  Одно и тоже множество может быть как упорядоченным, так и неупорядоченным в разных классах задач.

2)  Одно и тоже множество можно упорядочить различными способами.

Определение: Два упорядоченных множества считаются совпадающими, если они состоят из одних и тех же элементов, и если они упорядочены одним и тем же способом.

Размещения.

Определение: Пусть дано конечное множество , состоящее из  различных элементов. Размещением из  элементов по  элементам называется всякое упорядоченное подмножество множества  состоящее из  различных элементов.

Замечания:

Различные размещения отличаются или составом входящих в них элементов или порядком их расположения.

Теорема: Число различных размещений из элементов по  элементам вычисляются по формуле:

Пример: Имеется материал пяти различных цветов. Сколькими способами можно получить трехцветный флаг.

,

Перестановки.

Определение: перестановками из  элементов  называют различные упорядочения данного множества, состоящие из  элементов.  

Теорема: Число возможных перестановок из  элементов определяется формулой:

Доказательство:

Т.к. множество  является подмножеством множества  (), то перестановки из  элементов можно рассматривать как размещение из  элементов по  элементам. Поставим в формулу размещения .

Пример: Сколько различных четырехбуквенных  слов получается из слова «стол».

Сочетания.

Определение: Пусть дано конечное множество , состоящее из  элементов. Сочетанием из  элементов по  элементам называется любое  подмножество множества , состоящее из  элементов.

Замечание: Сочетания являются неупорядоченными подмножествами. Различные сочетания отличаются только составом элементов.

Теорема: Число всех сочетаний из  элементов по  элементам определяется по формуле:

Пример: Определить число различных шестизначных комбинаций.

Размещения с повторениями.

Определение: Размещением с повторением из  элементов по  элементам называется упорядоченное подмножество, состоящее из  элементов множества , причем элементы подмножеств не обязательно должно быть различным.