Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 18

Определение: Отношение  называется относительной частотой элемента .

Пример:

1:

2:

4:

Определение: статистическим рядом называют последовательность пар, обычно записываемых в виде таблицы.

			…
			…

Пример:

	1	2	4	5	6	7	8	9
	2	4	2	1	1	1	2	2

Определение: Статистическим распределением случайной величины  называют последовательность пар , также записываемых в виде таблицы.

Пример:

	1	2	4	5	6	7	8	9

Определение: При большом объеме выборки, ее элементы объединяют в группы, представляя результаты опыта в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки разбивают на  непересекающихся  интервалов. Потом определяют частоты  − количество элементов попавших в интервал. В верхнюю строку записывают  − середина интервала группировки, а в нижнюю частоты .

	[1,3]	(3,5]	(5,7]	(7,9]
	2	4	6	8
	6	3	2	4

Обычно после группировки также рассматривают накопленные частоты , относительные частоты , и накопленные относительные частоты .

Все результаты сводят в таблицу называемой таблицей частоты группированной выборки.

Замечание: Группировка выборки всегда вносит погрешность.

Интервалы
[1,3]	2	6	6
(3,5]	4	3	9
(5,7]	6	2	11
(7,9]	8	4	15		1

Графическое представление выборки.

Определение: Полигоном частот группированной выборки называется ломаная с вершинами в точках .

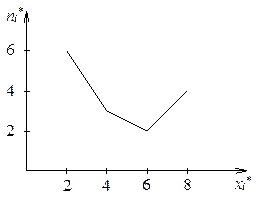
Определение: Полигоном относительных частот группированной выборки называется ломаная с вершинами в точках .

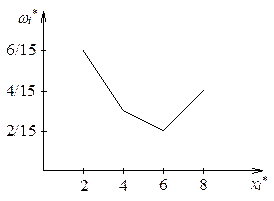
Гистограмма.

Определение: Гистограммой частот группированной выборки называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах так, что площадь каждого прямоугольника равна частоте . Площадь гистограммы равна объему выборки . Если длины интервалов одинаковы и равны , то высоты прямоугольников равны .

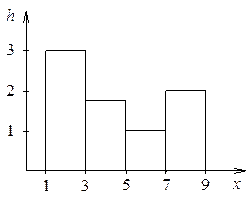
Гистограмма относительных частот строится аналогично,  но под ней площадь равна 1.

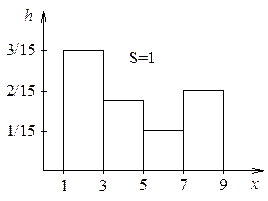
Определение: Полигоном накопления частот группированной выборки называется ломаная с вершинами в точках .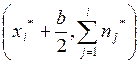

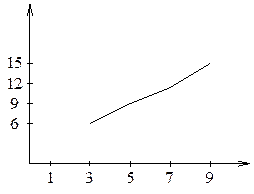
Определение: Полигоном относительного накопления частот группированной выборки кумулятивной кривой называется ломаная с вершинами в точках .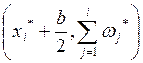

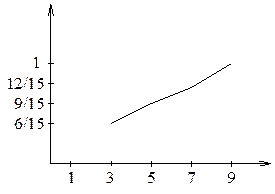
Определение: Эмпирической функцией распределения случайной величины  называется функция , определяющая для каждого значения   относительную частоту события .

, где  − число выборочных значений меньших ,  − объем выборки.

Определение: Функция распределения генеральной совокупности  называется теоретической функцией распределения.  определяется вероятность событий, а эмпирическая функция распределения  − относительную частоту этого события.

Из теоремы Бернулли следует, что при  эмпирическая функция  распределения сходится по вероятности к теоретической функции распределения. Т.е. при достаточно большом объеме выборки эмпирическая функция распределения и теоретическая функция распределения мало отличаются друг от друга.