Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 13

3) Пусть распределение случайной величины симметрично относительно точки , тогда .

Пример: Поиск математического ожидания.

1) Для равномерного закона:

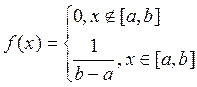
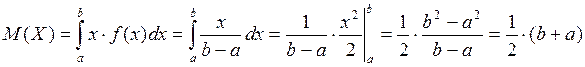
2) Показательное распределение

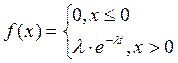
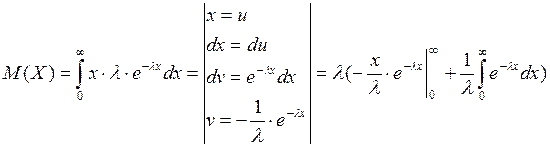
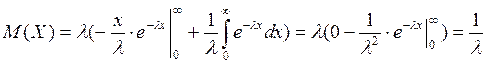
Пример: ДСВ задана следующим рядом распределения:

	-1	0	1	3	7
	0,3	0,2	0,1	0,2	0,2

Дисперсия

Определение: Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от е математического ожидания.

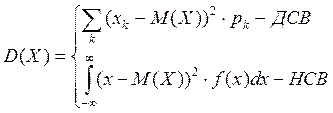
Свойства:

1) Дисперсия неотрицательна

2)

3)

4)

Дисперсия имеет размерность квадрата случайной величины.

Определение: Средним квадратичным отклонением случайной величины  называется неотрицательное число. Обозначается .

Пример: Найти дисперсию и отклонение для равномерного закона распределения.

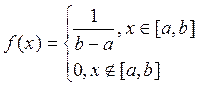
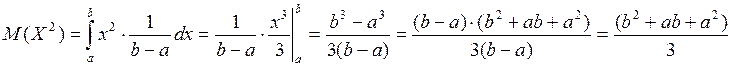
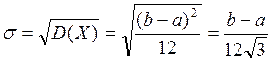 - среднее квадратичное отклонение

Пример: Найти дисперсию и среднее квадратичное отклонение.

	-1	0	2	3
	0,2	0,4	0,3	0,1

Определение: Начальным моментом -го порядка распределения случайной величины называется действительное число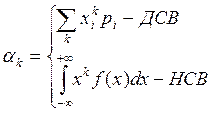

Замечание: Математическое ожидание является начальным моментом 1-го порядка.

Определение: Центральным моментом -го порядка распределения случайной величины  называется:

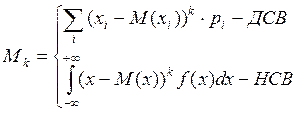
Замечание:  - есть центральный момент второго порядка.

Понятие индикатора события

С каждым случайным событием  из алгебры событий связана случайная величина

Определение:  называется индикатором события .

Свойства:

1)

2)

3)

4)

5)

Вычисление характеристик ДСВ принимающей целочисленные значения  методом производящих функций.

Пусть случайная величина принимает конечное или счетное число целочисленных значений. Поставим за данному распределению в соответствии функцию .

Функция  является аналитической в круге .

Определение: Функцию  называют производящей функцией для данного распределения вероятности.

	0	1	2	…

 

1) Биноминальное распределение.

2) Геометрическое распределение.

Т.к. , ,  сумма бесконечно убывающей геометрической прогрессии.

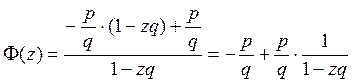
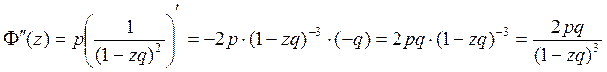
3) Распределение Пуассона.

Нормальное распределение

Определение: Нормальным распределением называется распределение по нормальному закону с параметрами  и , если ее плотность распределения вероятности имеет вид:

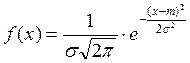
График функции  называется кривой Гаусса.

1)  причем  

2) Функция не является нечетной и не является четной

3) Функция непериодическая.

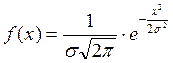Если , то функция  является четной и ее график симметричен относительно оси .

Т.к. заданная функция есть сдвиг четной функции на вправо, то ее график симметричен относительно прямой .

4)

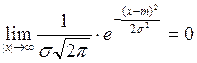
5)

 

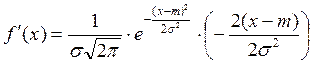
 критическая точка.

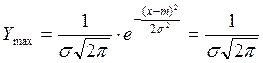
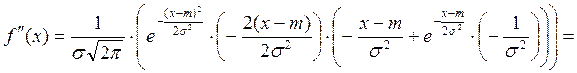
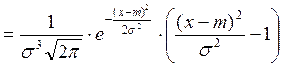
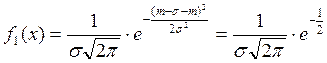
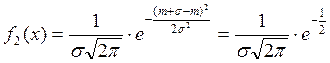
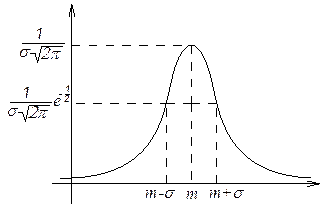
При изменении  кривая Гаусса не меняет своей формы, а смещается вдоль оси . При изменении :

1) при убывании  кривая растягивается в положительном направлении оси

2) при возрастании  кривая сжимается к оси

Т.к. график плотностей симметричен относительно оси , то , .

Пример: Составить нормальное распределение, если известно, что ,

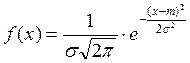
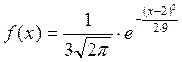
Определение: Нормированным называется нормальное распределение с параметрами , .

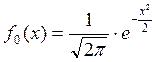
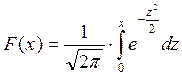 - функция Лапласа.

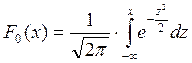 - функция распределения вероятности нормального закона

 - функция распределения вероятности нормированного нормального закона