Элементы математической логики. Нормальные виды формул. Совершенные нормальные формы, страница 4

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)                        - функция Шеффера

11)

12)

13)

14)                        - функция Вебба

15)

16)      - сложение по модулю 2; разделительная «или»

Обозначают

Таблица истинности для

1	1	0	1
1	0	1	0
0	1	1	0
0	0	0	0

Среди функций 0, 1, , , ,  «0» двойственно «1», «1» двойственно «0», «» двойственно «», «» двойственно «», «»двойственно «».

Для операции сложения справедливы следующие тождества:

1) 

2) 

3) 

4)  

5) 

6) 

7) 

Определение: Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных слагаемых, в которые все переменные входят не выше, чем в первой степени.

Теорема: Каждая булева функция может быть представлена многочленом Жегалкина.

Пример:

Для представления формулы в многочлен Жегалкина, формулу преобразовывают так, чтобы из логических символов осталась только конъюнкция и отрицание. Затем конъюнкцию заменяют умножением, отрицание прибавлением 1. Раскрывают скобки и преобразовывают выражение с использованием свойства 3.

, тогда многочлен:

Пример:

Многочлен:

Релейно-контактные схемы

Определение: Пусть  - набор контактов в электрической схеме. Контакт называется размыкающим, если когда напряжение не подается, он замкнут, и размыкается при подаче напряжения на обмотку реле, к которому он подключен. Контакт называется замыкающим, когда напряжение падает на обмотку реле.

В схеме один и тот же контакт может быть как замыкающим, так и размыкающим.

 если на обмотку подается напряжение

если на обмотку не подается напряжение

Определение: В любой схеме с контактами  ставится в соответствии функция проводимости:

Последовательному соединению контактов в алгебре логики соответствует операция конъюнкции.

Параллельному соединению контактов соответствует дизъюнкция.

Определение: Две схемы эквивалентны, если они одновременно проводят (или не проводят) ток на одноименные контакты реле.

Пример: Построить по формуле РКС.

и  - соединены параллельно.

Данной схеме соответствует схема:

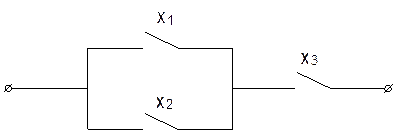
Пример:

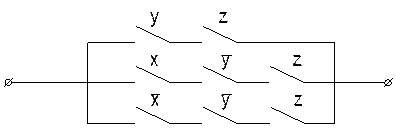
Составляем по данной схеме формулу:

Получаем:

Минимизация булевых функций.

Определение: Минимизация – это отыскание для заданной функции такой ДНФ, которая была бы наиболее простой по сравнению с другими.

Один из критериев простоты – минимальное количество переменных, причем при подсчете учитывается каждое вхождение переменной в формулу.

Определение: Элементарная конъюнкция  называется импликантой булевой функции , если не существует такого набора двоичных переменных, при котором , а .

В СДНФ любая элементарная конъюнкция – импликанта.

Определение: Элементарной конъюнкция называется простой  импликантой функции , если ни какая ее часть не является импликантой этой функции.

Определение: Сокращенная ДНФ называется ДНФ,  составленная только из  простых импликант.

Сокращенная ДНФ единственна, но не обязательно минимальна.

 - правило склеивания.

Алгоритм Квайна. Минимизация булевых функций.

1)  Представить булеву функцию в СДНФ

2)  Производя склеивание получить сокращенное ДНФ

3)  Исключить лишние импликанты

Определение:  Импликативной  матрицей называется матрица, в которой каждой строке соответствует прямая импликанта, а каждому столбцу элементарная конъюнкция, содержащая все переменные входящие в ДНФ.

Под элементарной конъюнкциями, в которые входит простая данная импликанта  ставится метка «1».

Алгоритм исключения лишних импликант.

1)  Выделение ядра Квайна:

Если в каком-либо столбце импликативной матрицы имеется только одна «1», то импликанта входит в ядро Квайна. Такая импликанта называется существенной. Вычеркивают строки с существенными импликантами и столбцы, покрываемые этими импликантами. Если в полученной матрице есть столбцы с одной «1», то операция повторяется.