Пусть ![]() − непрерывная случайная величина. Тогда
функция правдоподобия имеет вид:
− непрерывная случайная величина. Тогда
функция правдоподобия имеет вид:
![]() .
.
Пусть функция
![]() дифференцируема по
дифференцируема по ![]() . Тогда необходимое значение
. Тогда необходимое значение ![]() находят из условия:
находят из условия:
![]() .
.
Т.к. при
фиксированной выборке максимумы функции ![]() и
и ![]() совпадают, то:
совпадают, то:
![]() .
.
Если надо
оценить несколько параметров ![]() , то функция
правдоподобия:
, то функция
правдоподобия:
![]()
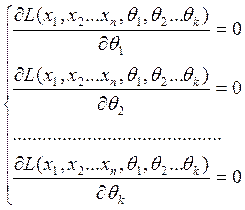
Свойства:
1) МП −
оценка является состоятельной оценкой параметра ![]() .
.
2) Эта ассиметрически эффективная оценка
3) Если для
параметра ![]() существует эффективная оценка, то
уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой.
существует эффективная оценка, то
уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой.
4) Решение
уравнения правдоподобия имеет ассиметрически нормальное распределение, т.е. при
соответствующей нормировки предельное распределение при ![]() полученной
оценки является нормальным.
полученной
оценки является нормальным.
Недостатки:
1) МП – оценка может оказаться смещенной.
2) Возможны очень сложные вычисления.
Пример: найти
методом моментов и методом максимального правдоподобия точечные оценки
неизвестных параметров ![]() и
и ![]() нормального
распределения.
нормального
распределения.
Метод моментов:
Приравняем начальные теоретические выборочные моменты и центральные теоретические выборочные моменты 2-го порядка.
Начальным теоретическим моментом является математическое ожидание:
![]()
Центральным теоретическим моментом является дисперсия:
![]()
Метод максимального правдоподобия:
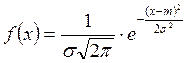
Функция правдоподобия:
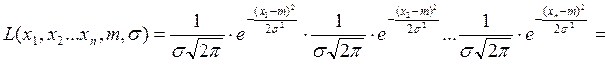
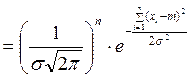
![]()
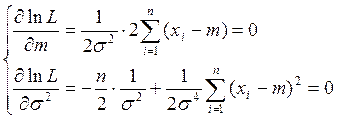
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Интервальные оценки.
Определение:
доверительным интервалом для параметра ![]() называется
интервал
называется
интервал ![]() , содержащий истинное значение параметра
, содержащий истинное значение параметра
![]() с заданной вероятностью
с заданной вероятностью ![]() .
.
Число ![]() называется доверительной вероятностью
или надежностью, а число
называется доверительной вероятностью
или надежностью, а число ![]() − уровнем
значимости.
− уровнем
значимости.
![]()
Левосторонний
доверительный интервал ![]() .
.
Правосторонний
доверительный интервал ![]() .
.
Обычно рассматривают симметричные доверительные интервалы, т.к. вероятность того, что:
![]()
![]() и
и ![]() −
являются функциями выборки, и длина доверительного интервала определяется
величинами: доверительной вероятностью и объемом выборки.
−
являются функциями выборки, и длина доверительного интервала определяется
величинами: доверительной вероятностью и объемом выборки.
Схема нахождения доверительного интервала.
1) Из
генеральной совокупности извлекается выборка объемом ![]() .
По ней методом моментов или методом максимального правдоподобия находится
точечная оценка
.
По ней методом моментов или методом максимального правдоподобия находится
точечная оценка ![]() неизвестного параметра.
неизвестного параметра.
2) Составляется некоторая статистика:
![]() , такая, что ее распределение не зависит
от
, такая, что ее распределение не зависит
от ![]() и других независимых параметров.
и других независимых параметров.
3) Задается доверительная вероятность
4)
Определяются значения ![]() и
и ![]() такие,
что:
такие,
что:
![]()
5) Решают
относительно ![]() неравенство:
неравенство:
![]()
1)
Доверительный интервал для математического ожидания нормального распределения
при известном ![]() .
.
Если
случайная величина ![]() распределена нормально, то
величина средняя выборочная
распределена нормально, то
величина средняя выборочная ![]() , также распределена
нормально с заданными характеристиками.
, также распределена
нормально с заданными характеристиками.
![]()
![]()
![]()
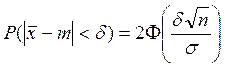
Обозначим
величину ![]()
![]()
Вероятность того, что
![]()
![]()
Из такого
равенства по таблице находим ![]() , и тогда раскрывая
модуль:
, и тогда раскрывая
модуль:
![]()
Вероятность
выполнения такого неравенства равна ![]() .
.
Следствие:
Если требуется найти математическое ожидание с наперед заданной точностью ![]() и вероятностью
и вероятностью ![]() ,
то минимальный объем выборки, который обеспечит эту точность, находится по
формуле:
,
то минимальный объем выборки, который обеспечит эту точность, находится по
формуле:
![]() .
.
Пример: Случайная
величина ![]() распределена нормально с
распределена нормально с ![]() . Найти доверительный интервал с
надежностью
. Найти доверительный интервал с
надежностью ![]() , если
, если ![]() .
.
![]()
![]()
![]()
Доверительный
интервал для математического ожидания нормального распределения при неизвестном
![]() .
.
По данным
выборки строится величина ![]() :
:
![]()
Эта величина
имеет распределение Стьюдента с ![]() степенями свободы.
степенями свободы.
Распределение
Стьюдента определяется только параметром ![]() и не
зависит от
и не
зависит от ![]() и
и ![]() .
.
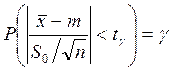
По заданному
значению ![]() и
и ![]() находят
находят
![]() . Получили следующий доверительный
интервал:
. Получили следующий доверительный
интервал:
![]()
Вероятность
выполнения такого неравенства равна ![]() .
.
Пример:
Случайная величина ![]() распределена нормально. По
выборке объемом 16.
распределена нормально. По
выборке объемом 16.
![]()
![]() .
.
Оценить
неизвестное математическое ожидание с доверительной вероятностью ![]() .
.
![]()
![]()
![]()
Проверка статистических гипотез.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.