Математика \ Математика

Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 9

· Реализация такого итерационного процесса на каждой итерации обращает в нуль максимальный недиагональный элемент матрицы.

Матрицей вращения называется матрица вида

то есть это единичная матрица, у которой на указанных местах стоят косинусы и синусы. Название “матрица вращения” связано с тем, что
в пространстве матрица является матрицей преобразования декартовых координат при повороте осей на угол . Непосредственным умножением можно убедиться, что .

В итерационном методе вращения строится бесконечная последовательность подобных преобразований с помощью матриц вращения так, чтобы в пределе исходная матрица преобразовалась к диагональному виду.

Предположим, что на некоторой k-й итерации построена матрица . Выбираем в ней максимальный по модулю внедиагональный элемент . Далее определяем угол преобразования из уравнения

(5.4)

По индексам i и j и углу строим матрицу вращения и выполняем преобразование матрицы . В результате получаем новую матрицу , отличающуюся от матрицы только элементами строк и столбцов с номерами i и j.

Выпишем соотношения для вычисления элементов матрицы, введя для упрощения промежуточную матрицу . Для элементов i-го и j-го столбца имеем:

(5.5)

Все остальные элементы для и . Теперь умножим слева на и получим матрицу . Для элементов i-й
и j-й строк имеем:

(5.6)

Все остальные элементы для и .

Можно показать, что в построенном процессе все внедиагональные элементы матрицы при достаточном числе преобразований становятся сколь угодно малыми.

Собственные векторы являются столбцами матрицы Здесь через K обозначено число вращений.

Контроль правильности вычислений на каждой итерации можно вести путем проверки сохранения следа матрицы . Следом матрицы называется величина 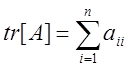. Тогда если сильно отличается от , то при переходе от к были допущены ошибки или велика
погрешность вычислений.

Алгоритм поиска максимального
по модулю собственного числа

Пусть матрица A неотрицательна. Обозначим максимальное по модулю собственное число матрицы A через и соответствующий собственный вектор через . Из курса линейной алгебры известно, что число совпадает с одной из норм матрицы A, т.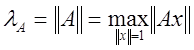е. , где .

Тогда алгоритм поиска имеет вид

1. задать ;

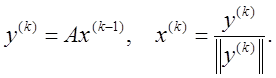
Теорема. Существуют пределы и для любого
начального приближения . При этом , .

Выбор начального приближения не представляет сложности, в качестве можно выбрать, например, вектор, у которого все компоненты
нулевые, а одна компонента равна единице.

Тема 6. Численное дифференцирование

Основные вопросы темы

1. Постановка задачи и дифференцирование многочлена Ньютона.

2. Безразностные формулы численного дифференцирования.

3. Применение ряда Тейлора для численного дифференцирования.

Задача численного дифференцирования возникает при нахождении производных от функции , заданной таблично, либо при нахождении производных от аналитической функции, непосредственное дифференцирование которой по каким-либо причинам затруднено. Важное приложение численного дифференцирования – разностная аппроксимация производных, которая широко используется при численном решении дифференциальных уравнений.

Общий подход к задаче численного дифференцирования состоит
в замене функции некоторой приближающей, легко вычисляемой функцией , , где – остаточный член приближения. Полагают, что , а – погрешность вычисления производной.

Наиболее распространенным является случай, когда в качестве приближающей функции выбирается интерполяционный многочлен. При этом производные соответствующих порядков легко определяются дифференцированием многочлена, а погрешность дифференцирования – дифференцированием остаточного члена или погрешности интерполяции, которая, согласно формуле (4.12), равна

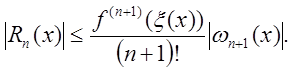
Для вывода формул численного дифференцирования удобно пользоваться многочленом в форме Ньютона, так как он содержит разделенные разности, являющиеся аналогами производных соответствующих порядков. Очевидно, что минимальное число узлов для получения k-й производной равно , так как дальнейшее дифференцирование многочлена степени k приводит к производной, равной нулю.

Представим функцию в виде

Тогда

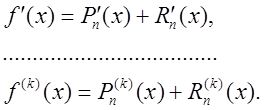
Для равноотстоящих узлов с шагом h имеем:

Таким образом, точность расчета производной при заданной степени многочлена уменьшается с увеличением порядка производной. При решении практических задач в основном приходится использовать аппроксимации первых и вторых производных. Значительно реже приходится аппроксимировать производные более высоких порядков.

Вычислим производную первого порядка с использованием многочленов первого и второго порядка:

	(6.1)
	(6.2)

При вычислении производной по формуле (6.1) максимальна ошибка в крайних точках отрезка и минимальна в середине. Погрешности
в точках и равны

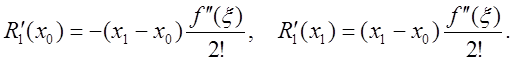
Согласно выражению (6.2) производная не является постоянной на отрезке . При равноотстоящих узлах максимальная погрешность имеет место в крайних точках, а минимальная – в средней, при этом ошибка дифференцирования равна

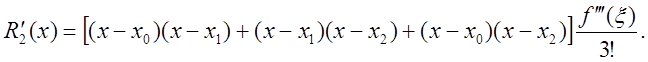
Вторая производная на отрезке является постоянной, равной

(6.3)

Погрешность вычисления второй производной имеет вид

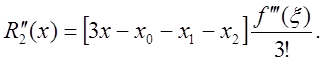
По-прежнему максимальная погрешность в вычислении имеет место
в крайних точках и минимальна в точке , но не равна нулю, поскольку мы имеем дело только с приближенными формулами. Отметим, что точки являются точками повышенной точности при вычислении производной k-го порядка.