Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 4

Развивая далее идеи аппроксимации функции, можно для построения итерационных формул использовать информацию о функции в нескольких точках, предшествующих точке   и строить квадратичную аппроксимацию по трем точкам, соответствующий метод называется методом парабол. Скорость сходимости метода парабол возрастает незначительно
по сравнению с методом секущих. Вместе с тем возникают задачи решения квадратного уравнения, выбора одного из корней многочлена и т.д.

Подробнее см.: 1, 3, 4, 5, 9.

Тема 3. Задача решения систем линейных уравнений

Основные вопросы темы

1 Постановка задачи и общие положения.

2. Метод исключения Гаусса.

3. Вычисления определителя и обратной матрицы методом Гаусса.

4. Метод прогонки.

5. Метод простой итерации. Метод Зейделя.

Требуется найти решение системы линейных алгебраических уравнений (СЛАУ)

(3.1)

где  – квадратная матрица коэффициентов при неизвестных размерности n;  – вектор-столбец неизвестных;  – вектор-столбец правых частей системы.

Для небольших значений n решение системы (3.1) не представляет сложности и может быть получено по правилу Крамера. Однако, если n велико, то для решения этим методом требуется приблизительно  операций типа умножения.

Вместе с тем линейные системы представляют собой большой интерес по двум причинам. Во-первых, к системам линейных уравнений приводят многие практические задачи. Во-вторых, важным и неиссякаемым источником СЛАУ являются практически все разделы вычислительной математики: нахождение решения СЛАУ необходимо в задачах уточнения корней систем нелинейных уравнений, аппроксимации функций, отыскания собственных значений и векторов матрицы, решения обыкновенных дифференциальных уравнений и т.д. Поэтому для быстрого решения систем большой размерности требуется построение новых методов.

Из курса линейной алгебры известно, что система (3.1) имеет единственное решение, если определитель , т.е. система уравнений является невырожденной. Если , то система не имеет решения
(при ) либо имеет неединственное решение (при ). С точки зрения практических вычислений существуют «почти невырожденные системы» – системы, определитель которых близок к нулю, но отличен от нуля.
Небольшие изменения коэффициентов матрицы системы или правых частей в «почти невырожденных системах» могут привести к большим
погрешностям решения. Системы такого типа называются плохо обусловленными.

Обусловленность системы характеризуется числом . Чем больше это число, тем хуже обусловленность системы; так,
при  система уже плохо обусловлена. Для вырожденных матриц .

Ниже будут рассмотрены наиболее известные прямые и итерационные методы. Из прямых методов будут рассмотрены метод Гаусса и метод прогонки. Из итерационных методов рассматриваются метод простой итерации и метод Зейделя.

Метод исключения Гаусса

Систему уравнений (3.1) представим в виде

(3.2)

или

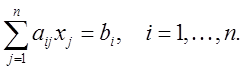
Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход),
а далее – к единичной матрице (обратный ход). Очевидно, что если
матрица A единичная, то .

Пусть матрица системы (1.3) – верхняя треугольная, поэтому  при , т.е. все элементы ниже главной диагонали равны нулю. Тогда
из последнего уравнения системы сразу определяем . Подставляя  
в предпоследнее уравнение, находим  и т.д.

Общие формулы имеют вид

(3.3)

Теперь опишем, как привести матрицу системы (3.2) к верхней треугольной матрице. Вычтем из второго уравнения системы (3.2) первое,
умноженное на такое число, что коэффициент при  обратится в нуль (нулю равен ). То же самое проделаем со всеми остальными уравнениями.
В результате все коэффициенты первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя второе уравнение, обратим
в нуль соответствующие коэффициенты второго столбца. Последовательно продолжая этот процесс, приведем матрицу системы к верхней треугольной форме.

Запишем общие формулы прямого хода метода Гаусса. Пусть проведено исключение коэффициентов из -го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:

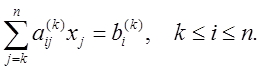
Умножим k-ую строку на число 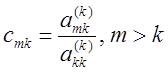 и вычтем из m-ой строки. Первый ненулевой элемент строки обратится в нуль, а остальные изменятся по формулам

(3.4) (3.5)

Проведя вычисления по этим формулам при всех указанных индексах, обратим в нуль элементы k-го столбца, лежащие ниже главной диагонали. Повторяя эту процедуру для других столбцов, приведем матрицу системы к верхней треугольной форме, при этом весь процесс приведения называется прямым ходом метода Гаусса. Вычисление неизвестных по формулам (3.3) называют обратным ходом метода.

На некотором шаге прямого хода метода может оказаться, что коэффициент , но мал по сравнению с остальными элементами матрицы и, в частности, мал по сравнению с элементами своей строки. Деление коэффициентов системы на малую величину может привести к значительным ошибкам округления. Для уменьшения ошибок поступают следующим
образом. Среди элементов k-го столбца  каждой промежуточной матрицы выбирают наибольший по модулю (главный) элемент и переставляют k-ую строку с i-ой строкой, содержащей главный элемент, затем проводят процедуру обнуления элементов столбца. Такая процедура метода исключения Гаусса называется методом Гаусса с выбором главного элемента. Для реализации метода требуется примерно  операций типа сложения и умножения.

Вычисление определителя и обратной матрицы
методом исключения

Определитель треугольной матрицы равен произведению диагональных элементов. В результате выполнения прямого хода метода исключения СЛАУ приводится к верхней треугольной матрице. Следовательно, определитель матрицы системы может быть вычислен как произведение:

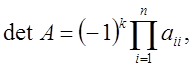
где k – количество перестановок строк при использовании метода
исключения с выбором главного элемента.

Для вычисления обратной матрицы воспользуемся тем, что , где E – единичная матрица. Обозначим элементы обратной матрицы
через . Тогда соотношение  можно записать в виде