4) Функция имеет вид ![]() , тогда уравнение Эйлера записывается
в форме
, тогда уравнение Эйлера записывается
в форме
|
|
(13.15) |
Это уравнение не является дифференциальным, если его решение удовлетворяет граничным условиям, то экстремаль существует.
5) Функция ![]() не зависит от t явно:
не зависит от t явно: ![]() , уравнение
Эйлера имеет вид
, уравнение
Эйлера имеет вид ![]() . Это уравнение имеет
первый интеграл
. Это уравнение имеет
первый интеграл
|
|
(13.16) |
Заметим, что часто непосредственное применение уравнения Эйлера оказывается проще, чем использование первых интегралов.
Теперь сформулируем достаточные условия экстремума. Для этого нам
понадобятся три понятия: условие Якоби, функция Вейерштрасса
и условие Лежандра.
Условие Якоби выполняется, если уравнение Якоби
|
|
(13.17) |
где ![]() – производные
подынтегральной функции, вычисленные на экстремали
– производные
подынтегральной функции, вычисленные на экстремали ![]() ,
удовлетворяющей уравнению Эйлера и граничным условиям, имеет решение
,
удовлетворяющей уравнению Эйлера и граничным условиям, имеет решение ![]() , которое:
, которое:
а) удовлетворяет условию ![]() ;
;
б) не обращается в нуль ни при каких значениях ![]() .
.
Функция
|
|
(13.18) |
называется функцией Вейерштрасса.
Условие ![]() называется условием
Лежандра, а условие
называется условием
Лежандра, а условие ![]()
![]() усиленным условием Лежандра. При
этом предполагается, что функция
усиленным условием Лежандра. При
этом предполагается, что функция ![]() трижды
дифференцируема по
трижды
дифференцируема по ![]() .
.
Достаточные условия слабого минимума
Если на экстремали ![]() , удовлетворяющей
уравнению Эйлера и граничным условиям, выполняется:
, удовлетворяющей
уравнению Эйлера и граничным условиям, выполняется:
а) условие Якоби;
б) либо условие Вейерштрасса: функция Вейерштрасса ![]() для точек
для точек ![]() ,
близких к
,
близких к ![]() , и для
, и для ![]() ,
близких к p; либо усиленное условие Лежандра на
,
близких к p; либо усиленное условие Лежандра на ![]() , тогда на
, тогда на ![]() достигается
слабый минимум.
достигается
слабый минимум.
Замечания: 1) если в условиях Вейерштрасса
и Лежандра поменять знаки неравенств на противоположные “![]() ” и “
” и “![]() ”,
то получатся условия слабого максимума; 2) условие Якоби в отдельности является
необходимым условием слабого экстремума, т.е. если
”,
то получатся условия слабого максимума; 2) условие Якоби в отдельности является
необходимым условием слабого экстремума, т.е. если ![]() обращается
в нуль при каком-нибудь значении
обращается
в нуль при каком-нибудь значении ![]() , то слабый
экстремум не достигается;
, то слабый
экстремум не достигается;
3) условие Вейерштрасса в отдельности является необходимым, т.е. если
в нем имеют место противоположные знаки, то слабый экстремум не достигается.
Достаточные условия сильного минимума
Если на экстремали ![]() ,
удовлетворяющей уравнению Эйлера и граничным условиям, выполняется:
,
удовлетворяющей уравнению Эйлера и граничным условиям, выполняется:
а) условие Якоби;
б) либо условие Вейерштрасса: функция
Вейерштрасса ![]() для точек
для точек ![]() , близких к
, близких к ![]() ,
и для произвольных
,
и для произвольных ![]() ; либо условие
; либо условие
Лежандра: ![]() для точек
для точек ![]() ,
близких к
,
близких к ![]() , и для произвольных
, и для произвольных ![]() , тогда на
, тогда на ![]() достигается
сильный минимум. Замечания здесь аналогичны замечаниям, сделанным выше.
достигается
сильный минимум. Замечания здесь аналогичны замечаниям, сделанным выше.
На основании изложенных необходимых и достаточных условий опишем общую схему нахождения экстремума функционала.
1. Найти экстремали ![]() , удовлетворяющие уравнению Эйлера
, удовлетворяющие уравнению Эйлера
и граничным условиям.
2. Проверить достаточные условия сильного
и слабого экстремума
на найденных экстремалях. Если достаточные условия выполняются, сделать вывод о
достижении сильного или слабого минимума или максимума. Если достаточные
условия не выполняются, учесть замечания 2) и 3).
В вариационном исчислении рассматриваются и более сложные задачи, в которых:
1) функционал зависит от нескольких
функций и их производных
порядка m;
2) кривые проходят через семейство граничных точек;
3) функционал содержит не только интеграл, но и некоторую функцию, называемую терминальным членом;
4) функции удовлетворяют, кроме граничных
условий, также дополнительным ограничениям в виде алгебраических,
дифференциальных
и интегральных уравнений.
Для всех этих задач также получены
необходимые и достаточные
условия экстремума, которые можно найти в [8, 10].
Подробнее см.: 8, 10.
Тема 14. Общие замечания
В ряде методов оптимизации, описанных
выше, предполагается,
что начальная точка ![]() , принадлежащая множеству X, известна. Для некоторых множеств таких, как параллелепипед,
шар, гиперплоскость, указать такую точку совсем нетрудно. Однако в общем случае
определение такой точки весьма непросто. Например, если
, принадлежащая множеству X, известна. Для некоторых множеств таких, как параллелепипед,
шар, гиперплоскость, указать такую точку совсем нетрудно. Однако в общем случае
определение такой точки весьма непросто. Например, если
|
|
(14.1) |
то для определения ![]() нужно
решить систему уравнений (вообще говоря, нелинейных). Чтобы найти точку
множества
нужно
решить систему уравнений (вообще говоря, нелинейных). Чтобы найти точку
множества
|
|
(14.2) |
придется решить систему неравенств.
Для
решения таких задач существуют специальные численные методы. Однако
полезно заметить, что задачу нахождения точки ![]() ,
принадлежащей множеству (14.1)
или (14.2), можно
сформулировать в виде задачи минимизации. А именно, в случае множества (14.1) введем функцию
,
принадлежащей множеству (14.1)
или (14.2), можно
сформулировать в виде задачи минимизации. А именно, в случае множества (14.1) введем функцию

а в случае множества (14.2) – функцию
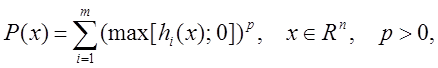
и рассмотрим задачу минимизации
![]() .
.
Для решения этой задачи могут быть
использованы любые подходящие методы минимизации. Если ![]() ,
то условие
,
то условие ![]() равносильно
равносильно
условию ![]() . Если
. Если ![]() ,
то
,
то ![]() . Если же
. Если же ![]() ,
,
но нижняя грань ![]() на
на ![]() не
достигается, то также
не
достигается, то также ![]() .
.
Если
![]()
то для
определения какой-либо точки ![]() можно рассмотреть
задачу минимизации
можно рассмотреть
задачу минимизации
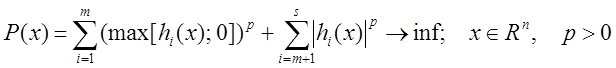 .
.
Задачу отыскания точки, принадлежащей множеству (14.2), можно свести к несколько иной задаче
![]() .
.
Понятно, что если ![]() ,
то
,
то ![]() . Определение начальной
. Определение начальной
точки ![]() не вызывает трудностей: достаточно
взять какую-либо точку
не вызывает трудностей: достаточно
взять какую-либо точку ![]() и положить
и положить ![]() . Для решения этой задачи можно
использовать, например, метод условного градиента. Итерационный процесс можно
прекратить, как только обнаружена точка
. Для решения этой задачи можно
использовать, например, метод условного градиента. Итерационный процесс можно
прекратить, как только обнаружена точка ![]() ,
для которой
,
для которой ![]() .
.
Выше были рассмотрены некоторые из
известных численных методов. Возникают естественные вопросы: чем
руководствоваться при выборе
метода для решения той или иной конкретной экспериментальной задачи, какой
метод является наилучшим? Иногда считают, что тот метод лучше,
у которого выше скорость сходимости на
некотором фиксированном классе задач. Однако при таком способе оценки
методов не учитывается такое важное качество, как трудоемкость каждой отдельно
взятой итерации
метода. Нередко бывает, что при решении конкретной задачи выгоднее применять
метод, который сходится не очень быстро и для получения
решения с необходимой точностью требуется довольно большое число итераций, но
тем не менее из-за того, что каждая итерация метода осуществляется просто,
суммарный объем вычислений и, следовательно, общее машинное время для получения
решения оказывается меньшим, чем при применении
другого быстросходящегося метода, каждая итерация которого весьма
трудоемка. Таким образом, при характеристике численного метода важнее
оказывается не скорость его сходимости, а общий объем вычислений, общее
машинное время, необходимое для получения решения с нужной точностью.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.