Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 17

ограничено. Тогда , множество  непусто, компактно и любая минимизирующая последовательность, принадлежащая , сходится к .

Подробнее см.: 2, 7.

Тема 11. Численные методы безусловной оптимизации

Основные вопросы темы

1. Необходимые и достаточные условия минимума.

2. Метод золотого сечения.

3. Градиентные методы.

4. Метод покоординатного спуска и метод Гаусса-Зейделя.

5. Метод сопряженных градиентов.

6 Метод стохастической аппроксимации.

Далее рассмотрим задачи безусловной оптимизации и методы их решения. Будем рассматривать задачу

.

(11.1)

Начнем с формулировки необходимых и достаточных условий
локального и глобального минимума. Для этого нам потребуется несколько определений.

Определение. Градиентом функции называется вектор , который обладает свойством: градиент перпендикулярен в каждой точке множества X касательной к линии уровня функции, имеющей уравнение , и направленный в сторону возрастания этой функции.

Определение. Точка x, в которой , называется стационарной точкой.

Определение. Матрицей вторых производных или матрицей Гессе функции  называется матрица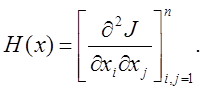

Теорема 1 [2]. (Необходимые условия локального или глобального минимума.) Если  есть минимум в (11.1) и функция  дважды непрерывно дифференцируема в этой точке и ее окрестности, тогда

1) ;	(11.2)
2) .	(11.3)

Замечание. Если функция  является непрерывно дифференцируемой, то необходимым условием минимума является только условие (11.2).

Теорема 2[2]. (Достаточные условия.) Пусть в точке  функция  
дважды непрерывно дифференцируема и , , тогда  есть точка локального минимума функции .

Следствие. Если в теореме 1 функция является также выпуклой на ,
то выполнение условий (11.2)–(11.3) является также и достаточным.

Аппарат необходимых и достаточных условий может быть использован для достижения двух целей. Во-первых, непосредственно для поиска
минимума. Сначала, используя условие (11.2), определяются стационарные точки  (определение связано с решением уравнения (11.2)), затем в этих точках проверяется условие . Этот способ мало применим, так как решение уравнения (11.2) обычно сложнее, чем численное решение задачи (11.1). Во-вторых, численное решение задачи (11.1) и проверка необходимых
и достаточных условий в точке окончания счета.

Для численного решения задачи (11.1) будем строить минимизирующую последовательность точек ,  по следующему алгоритму

.

(11.4)

a)  – начальная точка, задается как можно ближе к ;

b)  – величина шага;

c)  – возможное направление перехода от  к .

Не всякое направление , как видно из условия , является приемлемым. Нужно, чтобы

.

(11.5)

Сформулируем условие приемлемости направления :

(11.6)

Из (11.6) следует, что при  условие (11.5) выполнено, если

(11.7)

Условие (11.7) означает, что направление  – направление наибольшего убывания функции.

Конкретные методы решения (11.1) отличаются тем, что в них
используются различная информация о функции  и различные способы формирования  и . Можно указать два основных условия, которым подчиняется выбор  при заданном .

1) .

(11.8)

Выполнение условия (11.8) связано с вычислением  в каждой точке и изменением  при невыполнении условия.

2) Величина  выбирается в каждой точке  из условия , т.е. для каждого k нужно решить задачу одномерной минимизации.

Если шаг выбирается из условия 1), то процесс построения  называется процессом спуска, если из условия 2), то процессом наискорейшего спуска. Выбор первого или второго способа зависит от вида функции,
который определяет скорость решения одномерной задачи оптимизации.

На основании максимального порядка производной функции ,
который используется при формировании  и , методы делятся на методы нулевого порядка (используется только значение целевой функции), первого (используется значение функции и ее первой производной), второго
порядка и т.д.

На практике перед тем, как начать поиск оптимальной точки одним
из методов, требуется задать критерий окончания итерационного процесса и выбрать точность . В качестве критерия остановки можно выбрать одно из следующих условий:

1. ;

2. ;

3. .

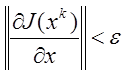Метод золотого сечения

Рассмотрим задачу одномерной минимизации

.

(11.9)

Задача (11.9) может быть решена численно, если функция  
на отрезке  строго унимодальная.

Определение. Функция  называется строго унимодальной
на отрезке , если она монотонна по обе стороны от единственной
оптимальной точки , т.е. выполнено

Метод золотого сечения состоит из двух этапов: 1) определения отрезка, содержащего точку минимума; 2) построения последовательности отрезков, стягивающихся к точке .

Алгоритм первого этапа

1. Выбираем точку  и определяем направление убывания функции . Для этого выбираем число h и вычисляем .
Если , то полагаем  и переходим к шагу 2 при . Если , то полагаем  и вычисляем .
Если , то полагаем  и переходим к шагу 2 при . Если , то полагаем  и повторяем процедуру этого
шага. В результате шага 1 получаем число h и точки  такие,
что .

2. Удваиваем h и вычисляем .

3. Вычисляем , если , то полагаем  и переходим к шагу 2. Если , то поиск прекращаем и в качестве
отрезка, содержащего точку минимума, выбираем .

Алгоритм второго этапа

1. Пусть найден отрезок , содержащий точку . Выбираем точность , с которой хотим определить точку ; величину ; вычисляем , , , , , ,  
и полагаем .

2. a) Если , то полагаем , , ,
вычисляем , ,  и переходим к шагу 3.

б) Если , то полагаем , , , вычисляем , ,  и переходим к шагу 3.

3. Если , то полагаем . Если ,
то  и переходим к шагу 2.

Обратим внимание на то, что на каждом шаге, за исключением первого, вычисляется только одно значение функции.

Утверждение [7]. При 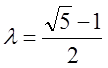 изложенный метод носит название
метода золотого сечения и порождает последовательность вложенных отрезков , стягивающихся к точке .