Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 3

Основные методы решения нелинейных уравнений являются итерационными, к их числу принадлежат метод дихотомии (половинного деления), метод Ньютона (метод касательных), метод секущих, метод парабол, метод простой итерации. Некоторые из этих методов будут рассмотрены подробно.

Важной характеристикой итерационных методов является скорость сходимости процесса. Говорят, что метод имеет n-й порядок сходимости, если 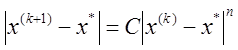, где С – постоянная, не зависящая от n. При  имеет место сходимость первого порядка, или линейная сходимость,
а при  – второго порядка, или квадратичная.

Итерационные методы позволяют получать решения с наперед заданной точностью, если доказана сходимость метода. Строго точного решения итерационные методы не дают, поскольку оно достигается как предел
последовательности (при ). Прямой метод, вообще говоря, дает точное решение, но из-за ошибок округления, имеющих место на любых компьютерах, оно не может быть достигнуто, причем заранее трудно оценить, насколько это решение отличается от точного. В связи с этим итерационные методы иногда позволяют получить решение с большей точностью, чем прямые.

Говорят, что метод является одношаговым, если для построения итерационной последовательности нужно вычислить функцию в одной точке, двухшаговым – в двух и т.д.

Сравнение различных методов следует проводить по числу операций при реализации одной итерации, т.е. при переходе от приближения  
к новому приближению , по скорости сходимости метода и по тем
условиям, которые необходимы для применения того или иного численного метода.

Метод деления отрезка пополам

Одним из итерационных методов поиска корня уравнения (2.1) является метод деления отрезка пополам (дихотомии).

Пусть действительный корень уравнения (2.1) отделен, т.е. имеется отрезок , внутри которого находится корень уравнения, и функция  непрерывна на интервале . Построим процесс сужения
интервала  так, чтобы искомый корень всегда находился внутри суженного интервала.

Алгоритм метода дихотомии.

1.  Пусть , .

2.  Выберем k-ое приближение , т.е. за  берется
середина отрезка.

3.  Вычислить произведения  и . Из двух
половин отрезка выбрать тот, где произведение является отрицательной величиной. Изменить одну из границ отрезка: , если выбрана первая половина отрезка или , если выбрана вторая половина.

4.  Увеличить k на 1 и перейти к шагу 2 алгоритма.

Таким образом, строится последовательность , сходящаяся
при  к .

Погрешность метода половинного деления определяется очевидным соотношением:

Процесс вычисления  продолжается до тех пор, пока погрешность метода  не станет меньше заданной точности , которая выбирается
заранее.

Достоинства метода: небольшие требования к функции , простота и надежность, всегда сходится, устойчив к ошибкам округления.

Недостатки метода: медленная скорость сходимости, не обобщается на системы уравнений.

Метод простой итерации

При использовании метода простой итерации для уточнения корня уравнение (2.1) заменяется эквивалентным уравнением

(2.2)

Это означает, что из  следует  и наоборот. Привести уравнение (2.1) к уравнению (2.2) можно многими способами, например, положив , где  – произвольная непрерывная знако-
постоянная функция.

Пусть известно начальное приближение  для значения корня , построим итерационный процесс

(2.3)

Утверждение. Если функция  имеет непрерывную производную,
то последовательность (2.3) сходится при выполнении условия

Замечание. Это условие является достаточным, т.е. если ,
то итерации могут расходиться, но если для начального приближения  
и всех  оно выполнено, то процесс (2.3) будет сходиться. Таким образом, в методе простой итерации важен выбор начального приближения.

Если на отрезке отделения корня выполнено условие ,
то погрешность на каждой итерации уменьшается для любого начального приближения не медленнее членов геометрической погрешности со знаменателем q. Метод простой итерации обобщается на системы линейных уравнений.

Метод Ньютона

Пусть функция  имеет непрерывную вторую производную
и задано  – приближение к корню. Заменим кривую  касательной к ней в точке  и определим значение  как точку пересечения касательной и оси абсцисс (рис. 1). В результате получим следующий итерационный алгоритм:

(2.4)

Этот метод носит еще одно название – метод касательных.

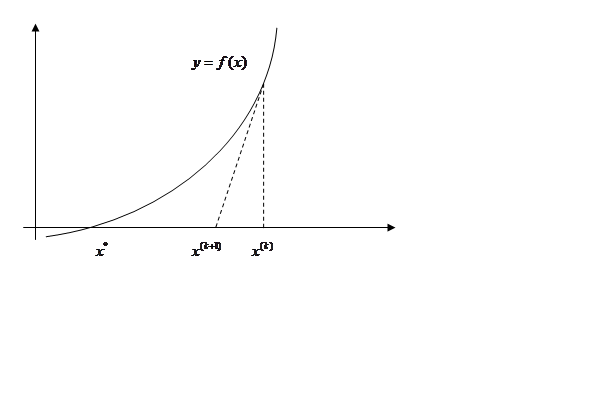
                                           Рис. 1

Достаточное условие сходимости метода Ньютона имеет вид:

Метод Ньютона вблизи корня имеет второй порядок сходимости:
на каждой итерации погрешность меняется пропорционально квадрату ошибки на предыдущей итерации.

Достоинства метода: квадратичная скорость сходимости, метод является одношаговым и может быть обобщен на системы уравнений.

Недостатки метода: большие требования к функции , расходится
в тех областях, где . Кроме того, если функция  задана таблично, то вычисление  сильно затруднено.

Последняя трудность устраняется в методе секущих.

Метод секущих

В методе секущих заменим вычисление производной  в формуле (2.4) приближенным значением, которое определяется по двум последним приближениям  и  соотношением

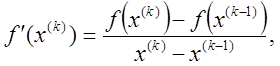
что приводит к замене касательной в точке  секущей, проведенной через две точки кривой  или, что то же самое, – к аппроксимации функции  на этом интервале линейной функцией (рис. 2).

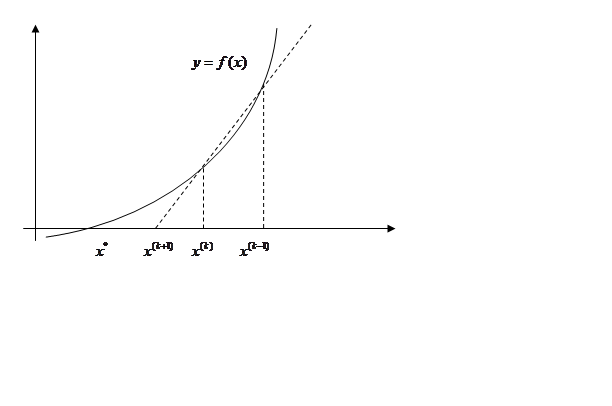
                      Рис. 2

Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона. К особенностям метода следует отнести следующие: сходится медленнее, чем метод Ньютона; не требует непосредственного вычисления производной на каждой итерации, что может привести к существенному уменьшению объема вычислений; метод является двухшаговым; сходимость метода может быть немонотонной даже вблизи корня.