Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 7

Эти формулы наиболее часто используются на практике. Если
задан  узел интерполяции, то на этих узлах можно построить один
интерполяционный степени и большой набор многочленов степени
меньше n, опирающихся на некоторые из этих узлов. Однако на практике наиболее часто используют многочлены не высоких степеней во избежание погрешностей в расчетах коэффициентов при больших степенях многочлена.

Интерполяционный многочлен в форме Ньютона

Интерполяционный многочлен в форме Ньютона представляет собой иную форму записи интерполяционного многочлена. Она имеет ряд отличий по сравнению с многочленом Лагранжа.

Для записи этого многочлена введем понятие разделенной разности. Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка  определяются через разделенные разности нулевого порядка:

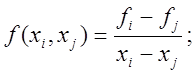
разделенные разности второго порядка определяются через разности первого порядка:

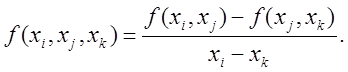
Продолжая этот процесс, получим разделенные разности порядка n:

(4.8)

Таким образом, для  точки могут быть построены разделенные разности до n-го порядка, разделенные разности более высоких порядков равны нулю.

Интерполяционный многочлен в форме Ньютона n-го порядка имеет вид

(4.9)

За точностью расчета удобно следить по убыванию величин членов суммы (4.9). Если величина членов убывает быстро, то оставляют только те из них, которые больше допустимой погрешности. Для повышения точности интерполяции в сумму могут быть добавлены новые члены, что требует подключения дополнительных узлов. При этом безразлично, в каком порядке подключаются новые узлы, и не требуется пересчета уже вычисленных разделенных разностей. Этим формула Ньютона выгодно отличается от формулы Лагранжа. Интерполяционный многочлен Ньютона удобен при построении формул численного дифференцирования и построения апостериорных оценок точности, т.е.  в процессе вычисления или после проведения интерполяции.

Приведем формулы линейного и квадратичного интерполяционного многочлена Ньютона:

	(4.10)
	(4.11)

Нетрудно убедиться, что эти формулы будут совпадать с соответствующими формулами для интерполяционного многочлена Лагранжа после простых преобразований. Очевидно, что это следствие единственности
интерполяционного многочлена.

Погрешность и сходимость интерполяции

Построив для функции  интерполяционный многочлен  
или , необходимо выяснить, насколько близко интерполяционный многочлен приближается к функции в других точках отрезка. Ошибку
интерполяции можно представить в виде

(4.12)

Теорема. Пусть n-ая производная функции  непрерывна на отрезке . Тогда для любой точки  существует точка , такая, что справедливо равенство

,   где  .

(4.13)

Так как точка  неизвестна, то обычно используют оценку сверху,
заменяя величины, входящие в (4.13), их максимальными значениями.
В результате получим следующую оценку погрешности

(4.14)

Формула (4.14) дает возможность провести априорную оценку точности, т.е. для случая аналитически заданной функции  провести оценку до начала вычислений. Однако так как величину производных интерполируемой функции бывает оценить достаточно сложно (например, для таблично заданной функции), то априорной оценкой пользуются редко. Удобнее применять апостериорную оценку по первому отброшенному члену многочлена Ньютона.

Отметим, что при увеличении числа узлов (степени многочлена) точность интерполяции не всегда возрастает. Это связано с тем, что функция  может не иметь  производной или максимум производной этой функции возрастает очень быстро с ростом степени n.

Задача об оптимальном распределении узлов на отрезке интерполяции, приводящая к минимизации ошибки интерполяции, решена П.Л. Чебышевым. Им показано, что если узлы интерполяции не распределены равномерно, а совпадают с корнями так называемых чебышевских полиномов степени , то ошибка многочленной интерполяции минимальна. Если интерполяция производится на отрезке , то узлы следует располагать следующим образом:

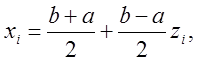
где .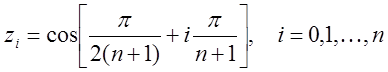

Интерполяция сплайнами

Использование одной интерполяционной формулы на большом числе узлов приводит к значительным погрешностям между узлами интерполяции. Одна из возможностей преодоления этого недостатка заключается
в применении сплайнов. Суть метода сплайн-интерполяции заключается
в определении интерполяционной функции по формулам одного типа для различных подмножеств и в стыковке значений функции и ее производных на границах подмножеств.

Будем строить между любыми двумя точками многочлен n-ой степени

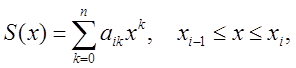
который в узлах интерполяции принимает значения интерполируемой функции и непрерывен вместе со всеми своими производными до  порядка включительно. Такой кусочно-непрерывный многочлен называется сплайном. Его коэффициенты находятся из следующих условий в узлах сетки: должны быть равны значения сплайна и приближаемой функции,
а также  производная соответствующих многочленов, при этом подразумеваются производные, взятые на соседних интервалах.

Максимальная по всем частичным отрезкам степень многочлена
называется степенью сплайна, а разница между степенью сплайна и порядком наивысшей непрерывной производной – дефектом сплайна (обычно обозначает через def).

Одним из наиболее распространенных интерполяционных сплайнов является кубический (). Этот многочлен представим как

(4.15)

Для построения кубического сплайна необходимо построить n многочленов третьей степени, т.е. найти 4n неизвестных . Эти коэффициенты ищутся из условий в узлах сетки, для этого нужно решить 4n уравнений. Пусть , тогда система уравнений имеет вид

	(4.16)
	(4.17)
	(4.18)
	(4.19)
	(4.20)
	(4.21)
	(4.22)