Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 21

Определение. Переменная  называется функционалом, зависящим от функции , если каждой кривой из заданного класса функций  соответствует действительное значение , т.е. функции соответствует число.

Далее будем использовать следующие классы функций:

1)  – непрерывные функции , определенные на отрезке  с нормой ;

2)  – непрерывные функции , имеющие непрерывные производные до порядка m включительно, определенные на отрезке  
с нормой .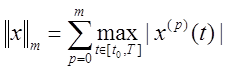

Определение. -окрестностью порядка m кривой  называется
совокупность кривых  такая, что

.

(13.1)

Кривые , на которых сравниваются значения функционала, называются допустимыми кривыми или кривыми сравнения. Через  будем обозначать допустимую кривую, на которой функционал достигает экстремума. Разность  называется вариацией кривой .
Используя вариацию , можно представить любую допустимую кривую в виде

,

(13.2)

где  – фиксированная функция;  – числовой параметр.

Используя вариацию , можно ввести определение вариации функционала. Будем называть величину

(13.3)

первой вариацией функционала, а величину

(13.4)

второй вариацией функционала.

Говорят, что функционал , определенный на классе  кривых , достигает на кривой  глобального минимума (максимума), если

.

Понятие локального экстремума связано с исследованием поведения функционала на близких кривых. Говорят, что функционал  достигает на кривой  слабого локального минимума (максимума), если  в -окрестности нулевого порядка кривой . Аналогично вводится понятие сильного локального минимума (максимума), если -окрестности кривой  будут первого порядка.

Приведем необходимые условия локального экстремума, которые совпадают для сильного и слабого экстремума.

Теорема 1 [8]. Если функционал , имеющий вариацию, достигает минимума или максимума на кривой , где  есть внутренняя точка
области определения функционала, то при  первая вариация функционала равна нулю

.

(13.5)

При выводе необходимых условий экстремума для различных задач вариационного исчисления используется следующая важная теорема.

Теорема 2 [10] (основная лемма вариационного исчисления). Если для каждой непрерывной функции

(13.6)

где функция  непрерывна на отрезке , то  на том же
отрезке.

Утверждение этой теоремы не изменится, если на функцию  наложить ограничения:  имеет непрерывную производную и .

Все изложенное выше без изменения переносится на функционалы , зависящие от вектор-функции одной переменной или зависящие от функций нескольких переменных.

Простейшая вариационная задача

Рассмотрим множество  допустимых функций , удовлетворяющим условиям:

а) функции  определены и непрерывно дифференцируемы
на отрезке , где  и  заданы, т.е. ;

б) функции  удовлетворяют граничным условиям

(13.7)

где значения  заданы, т.е. кривые проходят через две закрепленные граничные точки.

На множестве  задан функционал

(13.8)

где подынтегральная функция  имеет непрерывные частные производные до второго порядка включительно по всем переменным.

Среди допустимых кривых требуется найти кривую , на которой функционал (13.8) достигает экстремума, т.е.

(13.9)

Так как на кривые  не наложено дополнительных условий, кроме граничных, задача (13.9) называется задачей поиска безусловного экстремума.

Стратегия поиска решения задачи (13.9) состоит в определении
вариации  функционала и приравнивании ее к нулю согласно теореме
о необходимых условиях экстремума функционала. В результате получаются соотношения, позволяющие найти кривые, “подозрительные”
на наличие экстремума. С помощью анализа второй вариации функционала выводятся достаточные условия экстремума, позволяющие сделать вывод о достижении сильного или слабого минимума или максимума.

Найдем первую вариацию из выражения (13.3) и приравняем
ее к нулю:

,

(13.10)

где 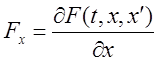,  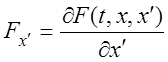– соответствующие производные
подынтегральной функции.

К выражению (13.10) применима основная лемма вариационного
исчисления, так как в силу условий задачи на кривой  функция 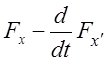 является непрерывной, а вариация  – произвольной непрерывно дифференцируемой функцией, удовлетворяющей условиям  . Следовательно, кривая , на которой достигается экстремум функционала, удовлетворяет уравнению

.

(13.11)

Уравнение (13.11) называется уравнением Эйлера. В развернутой форме уравнение (13.11) имеет вид

(13.12)

и при  представляет собой обыкновенное дифференциальное уравнение второго порядка. Его общее решение  определяет семейство экстремалей, а два граничных условия  позволяют найти произвольные константы  и  и, как следствие, кривую , на который может достигаться экстремум.

Теорема 3 [необходимые условия экстремума в задаче (13.9)]. Если на кривой , удовлетворяющей граничным условиям , достигается слабый экстремум функционала в задаче (13.6), то она удовлетворяет уравнению Эйлера (13.11). Если кроме того  имеет непрерывные частные производные до второго порядка включительно, то во всех точках , где , функция  имеет непрерывную вторую производную.

Краевая задача (13.11), (13.7) не всегда имеет решение, а если имеет, то не всегда единственное. Уравнение Эйлера интегрируется в квадратурах лишь в исключительных случаях. Приведем некоторые из них.

1) Функция  не зависит от x явно: , тогда уравнение Эйлера принимает вид 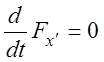 и, следовательно,

.

(13.13)

Соотношение (13.13) называется первым интегралом уравнения
Эйлера.

2) Функция  не зависит от t и x явно: ,
тогда уравнение Эйлера (13.9) записывается в форме . Его общее решение имеет вид

.

(13.14)

3) Функция  не зависит от t и  явно:  или
не зависит от  явно: , тогда задача (13.9) в общем случае решения не имеет, так как уравнение Эйлера принимает вид  
и не является дифференциальным, т.е. его решение не содержит произвольных констант и поэтому не удовлетворяет граничным условиям.
Однако если решение уравнения  проходит через граничные
точки  и , то экстремаль существует.