Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 14

Продемонстрируем эти этапы на примере решения задачи Коши для простейшего линейного уравнения первого порядка. Пусть требуется найти решение задачи Коши на интервале  для уравнения

(9.2)

Непрерывный интервал заменим множеством точек . Расстояние между точками h выберем постоянным. Величина h называется шагом разностной сетки. В общем случае эти шаги могут быть переменными. Для постоянного шага . Заменим дифференциальное уравнение разностным в точке :

(9.3)

Таким образом, первая производная аппроксимирована односторонней разностью вперед с первым порядком точности. Перепишем уравнение (9.3) в виде

(9.4)

Здесь , а . Из (9.4) следует, что

(9.5)

Из рекуррентного соотношения (9.5) имеем точное решение разностного уравнения (9.4)

(9.6)

Очевидно, что точное решение разностных уравнений можно получить лишь для простейших случаев. Точное решение задачи (9.2) имеет вид

Определим погрешность разностного решения. Имеем

Предполагая шаг разностной схемы малым, представим член 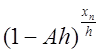 в виде

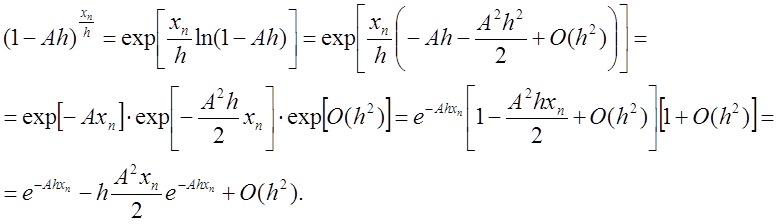
Подставляя это выражение в погрешность , получаем

(9.7)

Таким образом, величина погрешности имеет первый порядок точности и совпадает в данном случае с порядком аппроксимации производной. В общем случае порядок погрешности решения определяется не только порядком аппроксимации, но и порядком аппроксимации граничных условий.

Говорят, что разностная схема (9.3) имеет первый порядок точности на интервале. Можно показать, что на шаге эта разностная схема имеет второй порядок точности. Представим точное решение в виде ряда Тейлора в точке . Имеем

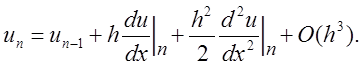
Поскольку

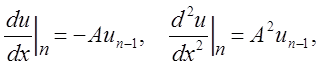
то

(9.8)

Из соотношений (9.5) и (9.8) следует, что погрешность на шаге имеет порядок . Очевидно, что погрешность на интервале выше на порядок, так как она накапливается по мере увеличения числа шагов. Отметим еще, что погрешность решения стремится к нулю, если , т.е. решение разностной задачи сходится к точному решению. Однако для сходимости
необходима не только аппроксимация дифференциального уравнения,
но и устойчивость разностной схемы. Не углубляясь в проблему устойчивости, отметим, что свойство устойчивости можно трактовать как равномерную зависимость решения разностной задачи относительно возмущений правых частей и граничных условий от шага h.

В теории разностных схем доказано, что разностная схема является сходящейся, если она обладает свойством аппроксимации и устойчива.

Метод Эйлера

Метод Эйлера является простейшим методом решения задачи Коши
и имеет невысокую точность, поэтому на практике его используют достаточно редко. Однако на его основе легче понять алгоритмы построения
более эффективных и более сложных методов.

Рассмотрим задачу Коши для дифференциального уравнения первого порядка

(9.9)

Обозначим границы отрезка a и b через  и  соответственно и введем на отрезке  сетку (в общем случае неравномерную) значений
аргумента x такую, чтобы выполнялось соотношение . Разложим решение  в окрестности узла сетки  по формуле Тейлора. Обозначив шаг сетки через  и  через , получаем

(9.10)

Если функция f имеет непрерывную p-ю производную, то в соотношении (9.10) можно оставить члены вплоть до . Эти производные можно найти, дифференцируя правую часть уравнения (9.9) требуемое число раз. Например, для первой и второй производной имеем

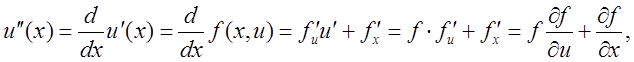
Аналогично можно получить производные более высоких порядков.

Однако использование формулы (9.10) с большим числом членов имеет ряд недостатков: во-первых, с ростом порядка производной выражение для нее становится сложным; кроме того, если функция f известна лишь приближенно или задана таблично, ее производные находятся с большой ошибкой. В связи с этим в разложении (9.10) оставляют только два члена. При такой замене вместо точного решения  получается его приближенное значение, которое находится по формуле

(9.11)

Так как значение  известно из начального условия, то, последовательно пользуясь формулой (9.11), находим приближенные решения . Формула (9.11) выписана для неравномерной сетки. Полагая шаг сетки  постоянным, получим

(9.12)

Формула (9.12) является основной формулой метода Эйлера или метода ломаных.

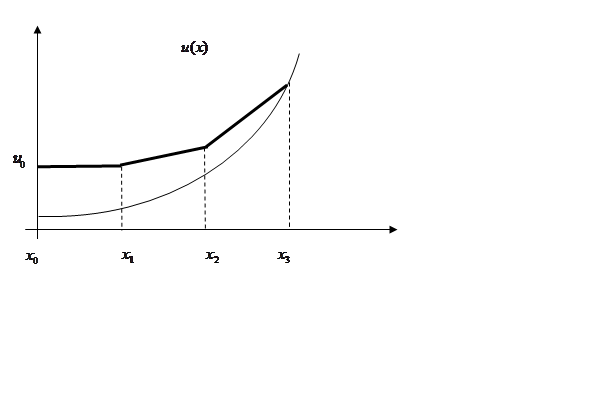
                                Рис. 4

Последнее название становится понятным из геометрической интерпретации итерационной схемы, представленной на рис. 4, на котором изображено семейство интегральных кривых уравнения (9.9). Как видно,
решение задачи Коши по методу Эйлера дает решение, не совпадающее
ни с одной из интегральных кривых, и является ломаной линией, совпадающей на каждом шаге с касательной к соответствующей интегральной кривой. Из рис. 4 следует, что метод Эйлера дает одностороннее приближение к точному решению . Сравнение формул (9.10) и (9.11) показывает, что метод Эйлера обладает вторым порядком точности на шаге, являясь в то же время методом первого порядка аппроксимации на интервале.

Существует несколько модификаций метода Эйлера. Остановимся
на одной из них – методе Эйлера с пересчетом. В этом методе значение  находится по формуле

(9.13)

т.е. вместо тангенса угла наклона касательной к интегральной кривой в точке , который имеет место в формуле (9.12), используется полусумма значений тангенсов углов наклона касательных в известной  
и искомой  точках. Поскольку значение  неизвестно, то (9.13) есть в общем случае нелинейное уравнение относительно , которое можно решать различными методами, предложенными во второй теме.

В рассматриваемом случае логично использовать метод простой итерации, поскольку нелинейное уравнение уже разрешено относительно . Тогда, если номер итерации обозначить верхним индексом, итерационный процесс запишется в виде

(9.14)

В качестве значения  можно принять любое , либо , т.е. использовать значение, вычисленное по формуле (9.12). Вычислим методом итераций только первое значение и остановимся. В результате получим