Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 5

(3.6)

где  – символ Кронекера,

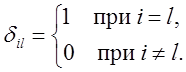
Видно, что если рассматривать l-й столбец обратной матрицы как вектор, то он является решением системы (3.6) с матрицей A и специальной правой частью, в которой на l-м месте стоит единица, а на остальных нули. Решение этой системы для каждого l дает элементы l-го столбца обратной матрицы. Таким образом, для обращения матрицы надо решить n систем линейных уравнений с одинаковой матрицей A и разными правыми частями. Приведение матрицы A к треугольной делается при этом только один раз,
а правые части преобразуются по формуле (3.5). Для обращении матрицы требуется совершить  операций.

Метод прогонки

Этот метод предназначен для решения СЛАУ с трехдиагональной матрицей коэффициентов при неизвестных. Этот случай является наиболее важным и распространенным случаем среди систем специального вида.
В таких системах отличны от нуля только элементы, лежащие на главной диагонали и на нижней и верхней диагоналях, прилегающих к ней.

Из-за специальной структуры матрицы в методе прогонки исключены операции с нулевыми элементами матрицы, что позволяет существенно сократить объем вычислений.

Запишем СЛАУ с трехдиагональной матрицей в виде

(3.7)

Прямой ход метода прогонки сводится к исключению неизвестного  в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестных  и  (кроме последнего уравнения, в котором содержится только ), и матрица ее – верхняя треугольная с двумя диагоналями. Обратный ход метода рассчитывается по рекуррентным формулам

(3.8) (3.9)

Величины  и  называются прогоночными коэффициентами
и вычисляются только по известным коэффициентам системы (3.7)
и известным предыдущим значениям  и . Для начала прямого хода
метода необходимо знать начальные значения коэффициентов  и ,
но поскольку , то можно задать любые значения для этих коэффициентов, обычно задают . Для начала обратного хода необходимо задать значение . Так как , то  и, следовательно, можно
задать любое значение . Обычно полагают , и тогда .

Достаточным условием корректности метода прогонки и устойчивости его к погрешностям является условие преобладания диагональных элементов:

Для реализации метода требуется примерно 8n операций. Отметим, что для трехдиагональных матриц .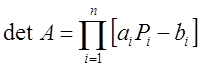

Метод простой итерации

В методе простой итерации система (3.1) уравнений  приводится к эквивалентной системе вида

.

(3.10)

Решение системы (3.10) и, следовательно, решение исходной системы ищется как предел последовательности векторов при :

(3.11)

где  – начальное приближение для вектора решения.

Достаточное условие сходимости метода простой итерации определяется следующей теоремой.

Теорема 1. Если какая-либо норма матрицы , согласованная с нормой вектора , т.е., меньше единицы , то последовательность  в методе простой итерации сходится к точному решению  системы (3.10)
со скоростью, не меньшей скорости геометрической прогрессии со знаменателем  при любом начальном приближении .

Следствие. Метод простой итерации сходится, если для матрицы  
выполняется одно из следующих условий:

(3.12)

Простейшим способом приведения системы (3.1) к виду (3.10), удобному для итераций, является выделение диагональных элементов, при этом каждое i-ое уравнение разрешается относительно i-го неизвестного:

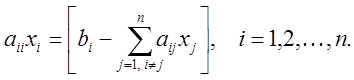
Матрица  при этом будет иметь вид

.

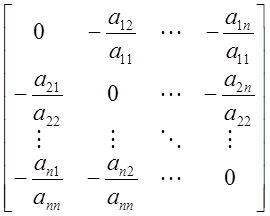Элемент этой матрицы можно записать в ви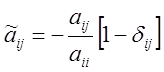де , где  – символ Кронекера. В этом случае достаточное условие сходимости метода может быть сформулировано как условие преобладания диагональных элементов матрицы A:

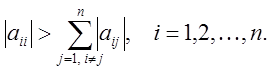
Еще раз заметим, что все рассмотренные формы условия сходимости являются лишь достаточными. Необходимым и достаточным условием сходимости метода простой итерации является условие того, что все собственные значения матрицы A по модулю меньше единицы.

Перейдем к вопросу об оценке погрешности решения. Представляют интерес два соотношения оценки погрешности решения : первое связывает погрешность с нормой разности двух последовательных приближений  и может быть использовано для оценки погрешности только в процессе вычислений; второе связывает погрешность
с нормой начального приближения  и вектора свободного члена . Необходимые соотношения даются следующей теоремой.

Теорема 2. Если какая-либо норма матрицы , согласованная с нормой вектора , меньше единицы , то имеют место следующие оценки
погрешности

(3.13)

Сделаем два замечания. Во-первых, соотношение (3.13) может быть записано в виде

.

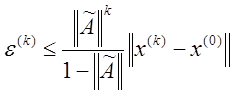Во-вторых, при использовании метода простых итераций в качестве оценки погрешности лучше не использовать норму разности двух последовательных приближений, так как из (3.13) следует, что если норма  близка к единице, то коэффициент при  может быть достаточно большим и оценка сверху (3.13) будет слишком грубой.

Погрешности последовательных итераций связаны соотношением

т.е. погрешность изменяется на шаге линейно. Вместе с тем количество итераций, необходимое для достижения требуемой точности, зависит
от значения  и начального приближения .

Метод Зейделя

В методе простой итерации не используется кажущаяся очевидной возможность улучшения сходимости итерационного процесса – немедленное введение в расчет вновь вычисленных компонент вектора . Эта возможность используется в итерационном методе Зейделя. Итерационный процесс для системы (3.10) выполняется при этом по соотношению

.

(3.14)

Не вдаваясь в подробности, отметим, что метод Зейделя часто действительно приводит к более быстрой сходимости, чем метод простой итерации. Однако возможны случаи, когда метод Зейделя сходится медленнее или вообще метод простой итерации сходится, а метод Зейделя расходится.

Отметим, что метод Зейделя сходится, если матрица A положительно определенная и симметричная.

Подробнее см.: 1, 3, 4, 5, 9.

Тема 4. Приближение функций

Основные вопросы темы