Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 8

Система (4.16)–(4.22) решается последовательно: сначала находятся  из уравнений (4.16), затем решается система (4.17)–(4.18), которая является трехдиагональной, следовательно, ее решение находится методом прогонки. Решив ее, находим затем коэффициенты  из уравнений (4.19)–(4.20) и  из уравнений (4.21)–(4.22).

Метод сплайн-интерполяции приводит к удовлетворительным результатам при аппроксимации непрерывных функций с гладкими первой и второй производными. При этом кубический сплайн будет обладать минимальной кривизной по сравнению с кривизной любой интерполяционной функции, имеющей непрерывную первую и вторую производные. Сплайн-интерполяция функций с резкими изменениями производных может давать большие ошибки. Сплайны более высокого порядка, чем третий, используются редко.

Метод наименьших квадратов

До сих пор рассматривалась интерполяция, т.е. способ приближения, когда значения приближаемой и приближающей функций совпадают
в узлах некоторой сетки. Однако достаточно часто, например, при аппроксимации большого числа экспериментальных точек, возможно найденных с некоторой погрешностью, такая интерполяция становится неразумной.
В этом случае лучше строить приближающую функцию таким образом, чтобы сгладить влияние погрешностей измерения и большого числа точек эксперимента. Такое сглаживание реализуется в методе наименьших квадратов (МНК). Метод позволяет использовать аппроксимирующие функции произвольного вида и относится к группе глобальных методов. Вид
аппроксимирующей функции определяется особенностями решаемой задачи, например, физическими соображениями, если проводится аппроксимация результатов физического эксперимента. Простейшим вариантом метода наименьших квадратов является аппроксимация полиномами, в частном случае прямой линией (полиномом первой степени). Этот вариант метода наименьших квадратов носит также название линейной регрессии. Кроме того, часто бывает, возможно, путем замены переменных свести задачу
к линейной (провести линеаризацию). Например, пусть аппроксимирующая функция ищется в виде . Прологарифмируем это выражение и введем обозначения, . Тогда в новых обозначениях задача сводится к отысканию коэффициентов линейной функции .

Рассмотрим полиномиальный вариант метода наименьших квадратов. Пусть функция  задана таблично в узлах , т.е. . Требуется построить многочлен 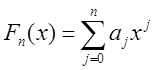. Критерием близости в методе наименьших квадратов является требование минимальности суммы квадратов отклонений от аппроксимирующей функции до экспериментальных точек:

(4.23)

Величина  называется среднеквадратическим отклонением.
Таким образом, не требуется, чтобы аппроксимирующая функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих погрешности. Далее, чтобы построить многочлен, требуется найти минимум функции J, выбирая коэффициенты .

Введем следующие обозначения:

,

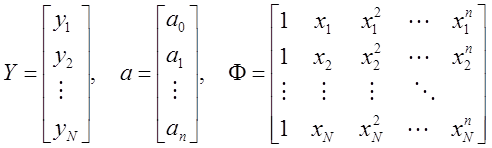тогда критерий можно записать в векторной форме

.

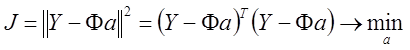Преобразуем критерий J:

Для поиска минимума воспользуемся необходимым условием экстремума:

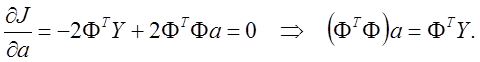
Здесь матрица  и вектор  являются известными. Полученная система линейных уравнений называется нормальной системой метода наименьших квадратов. Решив эту систему, мы найдем коэффициенты a и построим многочлен , приближающий функцию . Если , тогда

,

(4.15)

где матрица  имеет элементы

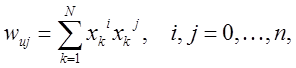
а вектор  имеет элементы

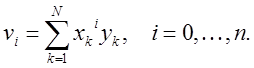
Если степень аппроксимирующего многочлена равна числу точек,
то метод наименьших квадратов совпадает с обычной интерполяцией,
поэтому МНК лучше применять, если .

Выпишем матрицу W и вектор V для :

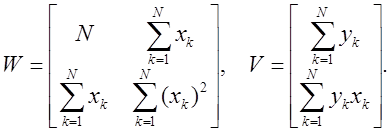
Далее подставляем эти данные в систему нормальных уравнений
и решаем систему из двух уравнений с двумя неизвестными.

Подробнее см.: 1, 3, 4, 5, 9.

Тема 5. Проблема отыскания собственных значений

Основные вопросы темы

1. Постановка задачи.

2. Метод вращения.

3. Алгоритм поиска максимального по модулю собственного числа.

Во многих задачах физики, химии, экономики и связанных с ними
задачах алгебры и вычислительной математики вместе с квадратной матрицей A порядка n приходится рассматривать уравнение

(5.1)

которое называют характеристическим уравнением матрицы A, и однородную систему

(5.2)

где E – единичная матрица порядка n,x – вектор-столбец.

Уравнение (5.1) есть алгебраическое уравнение степени n вида

(5.3)

Корни этого уравнения  называются собственными значениями (числами) матрицы A. Соответствующие каждому  ненулевые
решения x однородной системы (5.2) называются собственными векторами матрицы A.

С точки зрения линейной алгебры задача о собственных значениях
и векторах включает в себя: составление характеристического многочлена , решение уравнения (5.3); решение для каждого  системы (5.2), т.е. определение собственных векторов.

Говорят о полной проблеме собственных значений, если требуется определить все собственные значения и вектора матрицы, и о частичных проблемах, если требуется найти лишь отдельные собственные значения, например, максимальное или минимальное.

Итерационный метод вращения поиска собственных значений

Метод предложен в 1846 г. Якоби и позволяет решить полную проблему собственных значений для действительных симметричных матриц. В основе метода лежит тот факт, что действительная симметричная матрица может быть приведена подобным преобразованием к диагональному виду (диагональная матрица имеет собственные числа, совпадающие со значениями на диагонали). Метод Якоби основан на использовании нескольких идей.

·  Используется преобразование подобия , сохраняющее собственные числа.

·  При этом преобразовании используются ортогональные матрицы , приводящие матрицу A к диагональной матрице . Отметим,
что такая ортогональная матрица неизвестна и цель метода – получить ее.

·  В качестве ортогональной матрицы используется матрица вращения.

·  Итерационный процесс строится таким образом, чтобы после каждой итерации происходило уменьшение суммы квадратов недиагональных элементов.