Следовательно, пользуясь расчетом на сетке с шагом rh, удается оценить главный член погрешности расчета на сетке с шагом h. Если подставить найденную погрешность (7.13) в (7.12), то получим результат с более высокой точностью:
|
|
(7.14) |
Метод Ромберга может быть использован для
оценки погрешности расчета и получения результата с более высокой степенью
точности при решении различных задач, когда возможен расчет какой-либо величины
на сетках с различным шагом, например, при численном дифференцировании,
интегрировании, решении дифференциальных уравнений.
В качестве примера рассмотрим полученные
формулы численного
интегрирования, имеющие более высокий порядок точности. Проведем расчет
определенного интеграла по формуле трапеций с шагом 2h
(точки ![]() ,
, ![]() ),
а затем на сетке с шагом h (точки
),
а затем на сетке с шагом h (точки ![]() ,
, ![]() ,
, ![]() ). Обозначим
). Обозначим
результаты расчетов через ![]() и
и ![]() соответственно. Порядок точности
формулы трапеций равен двум, а сам остаточный член имеет такой же вид, как и в
формуле (7.11). Обозначая более точное значение через F,
проведем уточнение по формуле (7.14):
соответственно. Порядок точности
формулы трапеций равен двум, а сам остаточный член имеет такой же вид, как и в
формуле (7.11). Обозначая более точное значение через F,
проведем уточнение по формуле (7.14):
 Таким образом,
уточнение расчета формулы трапеций с использованием выражения (7.14) привело к
формуле парабол, имеющей более высокий – четвертый порядок точности.
Таким образом,
уточнение расчета формулы трапеций с использованием выражения (7.14) привело к
формуле парабол, имеющей более высокий – четвертый порядок точности.
Подробнее см.: 1, 3, 4, 5, 9.
Тема 8. Метод статистических испытаний
Основные вопросы темы
1. Постановка задачи и общие положения.
2. Моделирование случайных величин с заданным законом распределения.
3. Теоретические основы метода Монте-Карло.
4. Вычисление интегралов методом Монте-Карло.
При изучении численных методов основной
задачей являлось преобразование известной математической модели к виду,
допускающему
эффективное численное решение, т.е. сведение всех математических понятий
(производная, интеграл, дифференциальное уравнение и т.д.) к последовательности
элементарных арифметических операций. Для дальнейшего существенно, что вместе с
алгоритмом метода мы всегда получали оценку погрешности метода. Алгоритм
считался хорошим лишь в том случае, если малые погрешности, содержащиеся в
исходных данных и внесенные
в процессе преобразований или вычислений, не влияли неприемлемым
образом на результат вычислений. Процесс отыскания решения при таком подходе
являлся строго детерминированным, т.е. при повторении приводил к тому же
результату.
Однако существует целый ряд задач, для
которых разработка
и использование детерминированных методов оказывается практически невозможным и
нецелесообразным. Примером такой задачи может быть задача вычисления кратного
интеграла. Например, для вычисления пятикратного интеграла и обеспечения
приемлемой точности понадобится
более десяти миллиардов узлов.
Другой проблемой, возникающей при решении
практических задач, является то обстоятельство, что формулировка модели в виде
системы уравнений, допускающей численное решение, представляет значительные
сложности или оказывается невозможной. Такая ситуация является обычной при изучении реальных сложных систем,
состоящих из большого числа различных по природе и сложным образом
взаимодействующих элементов, функционирующих в условиях большого числа
случайных факторов. К сложным системам относятся крупные технологические и
производственные комплексы, экономические и социологические системы и т.п.
Одним из признаков сложных систем является принципиально вероятностный характер
их функционирования в условиях большого числа случайных факторов.
Общим способом решения таких проблем
являются методы статистических испытаний. С помощью этих методов задачи
решаются путем
моделирования случайных реализаций, имитации случайных процессов, происходящих
в сложных системах, с последующей оценкой их вероятностных характеристик.
Принято различать два основных класса методов статистических испытаний:
численные методы статистических испытаний (методы Монте-Карло) и
методы имитационного моделирования.
Суть численных методов статистических
испытаний заключается
в установлении связи между величинами, являющимися решением задачи (например,
значением интеграла) и вероятностными характеристиками
некоторого случайного процесса, такими, как вероятность, математическое
ожидание и др. Выбор конкретной случайной величины обусловливается
особенностями задачи. Существенной чертой методов Монте-Карло является
вероятностная оценка погрешности вычислений.
Суть методов имитационного моделирования заключается в моделировании физических представлений о реальном явлении или процессе функционирования системы.
Перечислим основные математические задачи, для которых построены вероятностные модели: вычисление кратных интегралов, решение систем линейных уравнений, обращение матриц, нахождение собственных значений и собственных векторов матриц, решение краевых задач и др.
Основные идеи метода Монте-Карло рассмотрим на двух простых примерах.
Предположим, что нам нужно вычислить площадь плоской фигуры S. Это может быть произвольная фигура с криволинейной границей, заданная графически или аналитически, связанная или состоящая из нескольких кусков. Пусть это будет фигура, изображенная на рис. 3, и пусть она вся лежит внутри единичного квадрата.
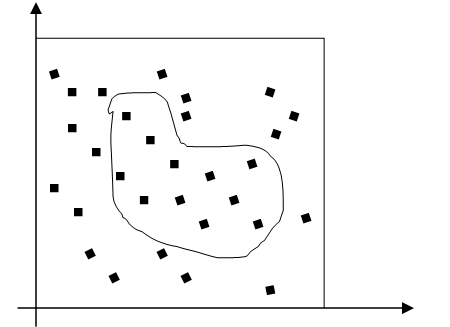
Рис. 3
Выберем внутри квадрата N случайных точек. Обозначим
через ![]() число точек, попавших внутрь S. Геометрически очевидно, что площадь S приближенно равна
число точек, попавших внутрь S. Геометрически очевидно, что площадь S приближенно равна ![]() . Чем больше N, тем больше точность этой оценки. В примере, изображенном на
рис. 3, выбраны 30 точек. Из них 11 оказались внутри S.
Отношение
. Чем больше N, тем больше точность этой оценки. В примере, изображенном на
рис. 3, выбраны 30 точек. Из них 11 оказались внутри S.
Отношение ![]() равно
равно ![]() ,
в то время как истинная площадь S равна 0,31.
Таким же образом можно вычислять объемы трехмерных
фигур и “многомерные объемы” тела в
многомерном пространстве.
,
в то время как истинная площадь S равна 0,31.
Таким же образом можно вычислять объемы трехмерных
фигур и “многомерные объемы” тела в
многомерном пространстве.
Второй пример – задача Бюффона, в которой
предложен случайный процесс, позволяющий вычислить число ![]() . Пусть имеется семейство равноотстоящих
параллельных прямых с расстоянием между прямыми, равным d,
и игла длины
. Пусть имеется семейство равноотстоящих
параллельных прямых с расстоянием между прямыми, равным d,
и игла длины ![]() .
.
При случайном бросании иглы ее средняя
точка может упасть на расстоянии x от какой-либо
прямой ![]() . Угол между иглой и нормалью к
прямой обозначим через φ. Игла пересекается с одной из прямых при
условии
. Угол между иглой и нормалью к
прямой обозначим через φ. Игла пересекается с одной из прямых при
условии ![]() для
для ![]() .
Вероятность такого положения иглы вычисляется по формуле
.
Вероятность такого положения иглы вычисляется по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.