Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 15

(9.15)

Формула (9.15) и есть основная формула метода Эйлера с пересчетом. Подобные схемы часто называют схемами типа прогноз-коррекция. Сначала по формуле (9.12) определяется прогнозируемое приближение решения, а затем по формуле (9.15) это решение уточняется.

Метод Эйлера с пересчетом обладает третьим порядком точности
на шаге и, соответственно, вторым порядком точности на интервале. Кроме того, он дает двустороннее приближение к решению.

Отметим, что поскольку нулевое приближение итерационного процесса задано, то процесс (9.14) можно продолжать до достижения заданной точности. Однако последующие итерации не повышают порядка точности схемы, и поэтому на практике используют одну-две итерации. Далее будет показано, что методы Эйлера являются частными случаями двухстадийных схем Рунге-Кутты.

Метод Рунге-Кутты

Метод Рунге-Кутты позволяет строить схемы различного порядка точности. Основная идея метода состоит в построении специального алгоритма – такого, чтобы приращение функции на шаге  совпадало с приращением , которое определяется из ряда Тейлора (9.10) с учетом возможно большего числа членов. При этом вторые и следующие производные определяются не дифференцированием, а путем многократного вычисления функции  в некоторых промежуточных точках между  и .

Проиллюстрируем основные идеи метода на примере получения схем второго порядка точности.

Оставим в разложении (9.10) члены вплоть до , имея в виду, что последний член разложения соответствует предполагаемому порядку точности схемы. Имеем

(9.16)

Чтобы избежать явного дифференцирования, заменим вторую производную  в соотношении (9.16) разностью

(9.17)

Величины ,  и  подбираются так, чтобы обеспечить нужный
порядок точности. Подставляя выражение (9.17) в (9.16), получаем

(9.18)

Полагая , , обозначая  и имея в виду,
что , и, следовательно, . С учетом того, что , перепишем выражение (9.18) в виде

(9.19)

Параметры α и δ определяются из условия наилучшего соответствия выражения (9.19) ряду (9.10). Принимая

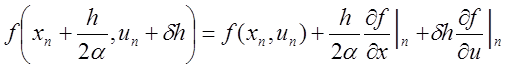
и, подставляя это соотношение в (9.18), имеем

(9.20)

Перепишем ряд (9.10) в виде

(9.21)

Из сравнения формул (9.20) и (9.21) видно, что первые три члена
в этих формулах совпадают, если . Выражая δ через α и подставляя в (9.19), получаем однопараметрическое семейство разностных схем Рунге-Кутты второго порядка точности. В результате

(9.22)

Схема (9.22) при  имеет третий порядок точности на шаге и второй на интервале. Из (9.20) можно получить рассмотренные разностные схемы. Так при  имеем метод Эйлера, выражаемый формулой (9.12), при  – первую итерацию метода Эйлера с пересчетом, а при  – так называемый метод хорд.

Аналогичным образом могут быть получены и схемы Рунге-Кутты более высокого порядка точности. В настоящее время наиболее распространена схема четвертого порядка точности, которая используется
в большинстве стандартных программ на компьютерах. Эта схема имеет вид

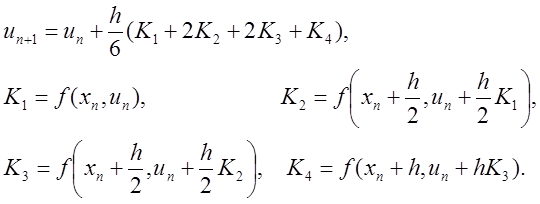
Многошаговый метод Адамса

В предыдущих схемах решение в точке  вычисляется с использованием решения только в одной точке . Логично предположить,
что можно повысить точность метода, если использовать информацию
о поведении решения в предыдущих точках . Такие методы получили название многошаговых.

Общая схема построения многошаговых методов выглядит следующим образом. Пусть нам известно приближенное решение в нескольких узлах сетки . Следовательно, в этих точках отрезка известно
и значение  правой части дифференциального уравнения (9.9)
при , причем  будет уже функцией только одной переменной . Заменим функцию  интерполяционным многочленом Лагранжа  и вычислим значение , проинтегрировав (9.9) на отрезке . Находим

(9.23)

Проведя интегрирование, находим разностную схему для решения дифференциального уравнения. Порядок схемы определяется величиной остаточного члена интерполяционного полинома.

В случае, когда для построения интерполяционного многочлена
используется четыре узла , получается формула Адамса,
которая на сетке с постоянным шагом записывается в виде

(9.24)

где .

Метод Адамса имеет четвертый порядок точности на интервале. Чтобы начать счет по формуле Адамса, необходимо знать решение в четырех
начальных точках .

По существу, интерполяционный многочлен  в формуле (9.23) используется вне области интерполяции, т.е. в данном случае это экстраполяционный многочлен. Однако поскольку интервал  мал,
то ошибка за счет экстраполяции невелика. Недостающие значения функции вычисляются в точках , как правило, по методу Рунге-Кутты соответствующего порядка, что является недостатком метода, так как увеличивает объем программы для компьютера. Преимущество многошаговых методов заключается в том, что на каждом шаге правая часть дифференциального уравнения вычисляется только один раз, а в методе Рунге-Кутты четвертого порядка точности на каждом шаге функция вычисляется четыре раза. Здесь, естественно, необходимо учитывать соотношение
шагов двух методов, обеспечивающих заданную точность. В случае, когда правая часть дифференциального уравнения является функцией только
одной переменной x, остаточный член в формуле Рунге-Кутты четвертого порядка точности на равномерной сетке равен остаточному члену  формулы трапеций численного интегрирования с шагом , следовательно

В формуле Адамса остаточный член

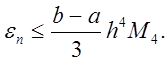
Таким образом, остаточный член в первом случае на три порядка меньше чем во втором. Следовательно, для получения результата с одной
и той же точностью можно шаг в методе Рунге-Кутты брать примерно
в шесть раз большим, чем в формуле Адамса.

Достоинство метода Адамса по сравнению с методом Рунге-Кутты
заключается в простоте оценки остаточного члена метода.

На этом мы закончим рассмотрение численных методов решения дифференциальных уравнений. В заключении заметим, что существуют также численные методы решения краевых задач и дифференциальных уравнений в частных производных.