Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 16

Подробнее см.: 1, 3, 4, 9, 10.

Тема 10. Задача оптимизации

Основные вопросы темы

1. Постановка задачи и вспомогательные сведения.

2. Существование экстремума.

Оптимизация – процесс нахождения экстремума (глобального минимума или максимума) некоторой функции или выбор наилучшего (оптимального) варианта из множества возможных. Приведем математическую формулировку задачи.

Необходимо найти минимум скалярной функции  векторного
аргумента x на множестве

,

где  и  также скалярные функции.

В дальнейшем будем говорить о поиске минимума функции ,
так как поиск максимума  сводится к поиску минимума функции .

Функция  называется целевой функцией; множество X – множеством допустимых решений или областью определения, а решение  
задачи оптимизации – оптимальной точкой.

Определение. Говорят, что функция  достигает глобального минимума на множестве X, если , ; величину  называют наименьшим или минимальным значением  на X и обозначают . Множество всех точек минимума  на X будем обозначать .

В зависимости от свойств множества X и функции  множество  может содержать одну, несколько или даже бесконечно много точек,
а также возможны случаи, когда  пусто.

Определение. Говорят, что функция  достигает в точке  
локального минимума, если , .

Глобальный минимум является локальным, но его -окрестность – вся область определения. Функция на множестве X может иметь несколько глобальных и локальных минимумов, однако наименьшее значение функции  в точке глобального минимума единственное.

Определение. Говорят, что функция  ограничена снизу на X, если  . Функция  неограничена снизу на X, если существует последовательность , для которой .

В тех случаях, когда , естественным обобщением понятия наименьшего значения функции является понятие нижней грани функции.

Определение. Пусть  ограничена снизу на X. Тогда число  называют нижней гранью  на X, если: 1)  при всех ; 2) для
любого сколь угодно малого числа  найдется точка , для которой . Если функция не ограничена снизу на X, то в качестве нижней грани принимается значение . Нижнюю грань обозначают через .

Если , то нижняя грань  на X совпадает с наименьшим значением этой функции, т.е. . В этом случае говорят,
что функция достигает своей нижней грани. Подчеркнем, что  всегда существует, а  не всегда имеет смысл. Введем еще два определения.

Определение. Последовательность  называется минимизирующей для функции  на множестве X, если

Из определения и существования нижней грани следует, что минимизирующая последовательность всегда существует.

Определение. Скажем, что последовательность  сходится к непустому множеству X, если , где  – расстояние от точки  до множества X.

Заметим, что если , то всегда существует минимизирующая
последовательность, сходящаяся к . Например, можно взять последовательность  где  – какая-либо точка из . Однако
не следует думать, что при  любая минимизирующая последовательность будет сходиться к .

В силу введенных определений можно говорить о задачах двух типов. К первому типу относятся задачи, в которых требуется определить величину . Сразу подчеркнем, что в этих задачах неважно, будет ли множество  точек минимума непустым или оно пусто. Ко второму типу задач отнесем те задачи, у которых множество  не пусто и требуется
наряду с  найти какую-либо точку .

Заметим, что получить точное решение задачи первого или второго типа удается лишь в редких случаях. Поэтому на практике при решении задач первого типа обычно строят какую-либо минимизирующую последовательность  и затем в качестве приближения для  берут величину  при достаточно большом k. Аналогично для приближенного решения задач второго типа при достаточно большом k берется  и точка .
В дальнейшем будем рассматривать в основном задачи второго типа.

Математическая запись задачи оптимизации имеет вид

.	(10.1) (10.2)

Задачи оптимизации можно разбить на группы:

·  задачи безусловной оптимизации. В этом случае ищется минимум целевой функции, а ограничения на вектор x не накладываются, т.е. ;

·  задачи условной оптимизации линейного программирования.
В этом случае целевая функция  и дополнительные условия  и  линейны;

·  задачи условной оптимизации нелинейного программирования.
В этом случае либо целевая функция, либо одно из ограничений нелинейно;

·  задачи вариационного исчисления. В этом случае ищется экстремум не функции, а функционала.

Существование экстремума

Для некоторых классов задач второго типа любая минимизирующая последовательность сходится к . Один из таких классов задач описан
в теореме Вейерштрасса. Для формулировки этой теоремы нам понадобятся понятия компактного множества и полунепрерывной снизу функции.

Определение. Множество X из  называется компактным, если
любая последовательность  имеет хотя бы одну предельную точку v, причем .

Известно, что всякая ограниченная последовательность ( для всех ) имеет хотя бы одну предельную точку. Поэтому в  компактными являются все замкнутые и ограниченные множества и только они.

Определение. Пусть функция  определена на множестве . Говорят, что функция  полунепрерывна снизу в точке , если для любой последовательности , сходящийся к точке x, имеет место
соотношение 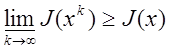. Другими словами, если для любого  
существует  такое, что для всех  справедливо
неравенство .

Очевидно, что непрерывная функция является полунепрерывной снизу.

Теорема 1 [2]. Пусть X – компактное множество, а функция  
определена, конечна и полунепрерывна снизу на X. Тогда , множество  не пусто, компактно и любая минимизирующая последовательность сходится к .

Заметим, что в теореме 1 условие компактности множества X является довольно жестким. Например, такие множества, как  – все пространство или  – неотрицательный ортант, не являются компактными. Приведем теорему, в которой нет требования компактности, но зато функция  удовлетворяет дополнительным требованиям.

Теорема 2 [2]. Пусть X – непустое замкнутое множество из ,
функция  конечна, полунепрерывна снизу на X и для некоторой фиксированной точки  множество Лебега