Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 12

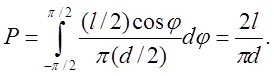
Одновременно по теореме Бернулли эта же вероятность 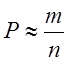, где n – число бросаний иглы, m – число пересечений иглы одной из прямых.
Таким образом, приближенное вычисление числа  имеет вид

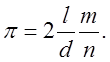
Задача Бюффона интересна тем, что позволяет сформулировать
основные проблемы и особенности метода статистических испытаний.

Во-первых, простая структура вычислительного алгоритма.

Во-вторых, общая схема метода статистических испытаний такова: выбирается такая процедура случайного испытания, чтобы какая-либо
вероятностная характеристика случайной величины равнялась искомой
величине или очевидным образом была с ней связана.

В третьих, отметим, что вычисление числа  с использованием предложенного метода потребует большого числа бросаний для обеспечения вычисления числа  с точностью, например, до двух знаков. При решении практических задач длина используемых последовательностей случайных чисел исчисляется сотнями тысяч или миллионами. Поэтому практическое использование метода статистических испытаний определяется двумя факторами: наличием простых и экономичных способов формирования последовательностей случайных чисел и возможностью организации эффективных испытаний.

И последнее, погрешность вычислений, как правило, пропорциональна , где D – некоторая постоянная, а N – число испытаний.
Отсюда видно, что для уменьшения погрешности в десять раз (т.е. чтобы получить в ответе еще один верный десятичный знак) необходимо увеличить число испытаний в 100 раз.

Моделирование случайных величин
с заданным законом распределения

Для выработки последовательностей случайных чисел существуют
генераторы псевдослучайных чисел, которые генерируют случайные вели
чины, имеющие стандартные законы распределения. Если требуется получение нестандартных случайных величин, то в настоящее время существует
несколько схем получения таких последовательностей. Рассмотри одну
из них.

В качестве исходной рассматривается последовательность случайных чисел с равномерным законом распределения на отрезке . Путем функциональных преобразований конструируются случайные последовательности практически с любым законом распределения. Идею метода проиллюстрируем на примере. Пусть имеется дискретная случайная величина,
с конечным числом реализаций, заданная рядом распределения

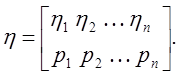
Отрезок  разобьем на n частей так, чтобы длина каждого была равна . Выбирая из последовательности равномерных величину , фиксируем, в какой интервал попадает это значение. В зависимости от этого полагаем значение случайной величины , где i – номер подынтервала, в который попала случайная величина .

Такой метод формирования случайных величин для непрерывных случайных величин носит название метода обратной функции. Суть метода заключается в следующем. Пусть непрерывная случайная величина  
задана непрерывной и строго монотонной функцией распределения

где  – плотность распределения вероятностей. Тогда значение  будем вычислять из уравнения  по формуле , где  имеет равномерное распределение на отрезке . Или по-другому, если требуется найти распределение  на отрезке , то значения  можно находить из уравнения

(8.1)

Рассмотрим пример. Пусть требуется получить последовательность случайных величин , имеющих экспоненциальный закон распределения

Тогда уравнение для отыскания  имеет вид . Разрешая это уравнение относительно , придем к выражению

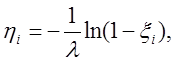
где  – реализация равномерной случайной величины из отрезка .

Теоретические основы метода Монте-Карло

Теоретическую основу метода статистических испытаний составляют теоремы теории вероятностей – теорема Чебышева, центральная предельная теорема и теорема Бернулли.

Теорема Чебышева. Пусть  – независимые случайные величины
с математическим ожиданием  и с равномерно ограниченной дисперсией. Тогда

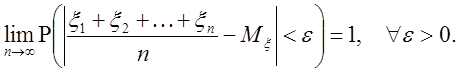
Или в другой форме записи для нормального закона распределения получаем центральную предельную теорему

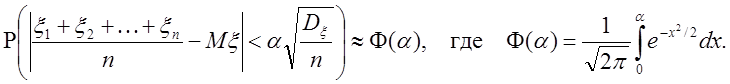
Теорема Чебышева утверждает сходимость по вероятности среднего арифметического n случайных величин к их математическому ожиданию при .

Теорема Бернулли. Если некоторое событие A может наступить в каждом m из n независимых испытаний с вероятностью p и при этом , тогда

Таким образом, по теореме Бернулли при неограниченном увеличении числа испытаний оценка вероятности  случайного события сходится к истинному значению вероятности.

Вычисление интегралов методом Монте-Карло

Вычисление определенных интегралов – одна из наиболее распространенных задач, решаемых методом Монте-Карло. Практическая ценность метода для вычисления кратных интегралов в том, что порядок сходимости метода статистических испытаний не зависит от кратности интеграла. Известно несколько вероятностных схем решения задачи
о вычислении интеграла. Рассмотрим основные идеи метода, оценку
погрешности и некоторые приемы повышения эффективности процедуры решения.

Пусть требуется вычислить интеграл

(8.2)

где  – функция, заданная на S-мерной гиперплоскости, u – координаты точки на этой гиперплоскости и G – область на этой гиперплоскости.

Приведем интеграл (8.2) к виду

(8.3)

и введем случайную величину  с плотностью вероятностей  
и случайную величину , являющуюся функцией случайной величины . Математическое ожидание  и дисперсия  случайной величины  равны

	(8.4)
	(8.5)

Функцию  следует выбирать так, чтобы она была как можно ближе к , поскольку в этом случае  будет минимальна. Выбрать эту функцию в точности равной  невозможно, так как для этого нужно знать значение интеграла 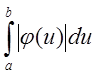, а сложность вычисления этого интеграла равноценна решению исходной задачи.

Пусть имеется последовательность независимых в совокупности случайных величин . Согласно центральной предельной теореме, среднее арифметическое значений функции  по всей совокупности
точек не зависит от функции распределения случайной величины  и является случайной величиной, распределенной по нормальному закону
при . На основании теоремы Чебышева и на сравнении соотношений (8.3) и (8.4) получаем, что интеграл  можно рассматривать как математическое ожидание случайной величины , т.е.